Hi Michael,

I am going to do a slightly different problem. The instructions are the same but the function is

g(x) = 3x⁵ - 20x³.

The zeros are the points where 3x⁵ - 20x³ = x³(3x² - 20) = 0. x = 0 is a zero three times and there are two others, x = ±√(20/3).

For the remainder of the problem you need the derivative of g(x).

g'(x) = 15 x⁴ - 60 x² = 15x²(x² - 4) = 15x²(x - 2)(x + 2)

I then want to solve g'(x) = 0 which gives me

x = -2, 0, 2

The sign of the derivative tells us in the function is increasing or decreasing. Since the derivative is continuous it can only change sign by passing through zero. Hence the three zeros above divide the line into 4 parts, (less than -2, between -2 and 0, between zero and two and greater than 2) and g(x) is either increasing or decreasing in each of these parts. Hence I only ned check at one one point in each of the four parts of the line.

g'(-3) = 15 × (-3)² × (-3 -2) × (-3 + 2) is positive and hence g(x) is increasing for x < -2.

g'(-1) = 15 × (-1)² × (-1 -2) × (-1 + 2) is negative and hence g(x) is decreasing for -2 < x < 0.

g'(1) = 15 × (1)² × (1 -2) × (1 + 2) is negative and hence g(x) is decreasing for 0 < x < 2.

g'(3) = 15 × (3)² × (3 -2) × (3 + 2) is positive and hence g(x) is increasing for 2 < x.

Therefore g(x) has a relative maximum at x = -2 and a relative minimum at x = 2.

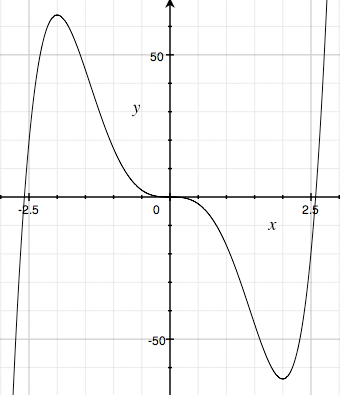
g(x) = 3 x⁵ - 20 x³

Harley