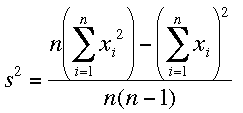Incremental standard deviation

Math Central

Quandaries & Queries

In relation my question asked earlier, i would first like to thank you for the prompt reply. But it has not answered my query yet. Let me frame the problem again.

I have a mean value for N data items. (note that i know N but i donot know the distinct N data item values) Now the (N+1)th data item comes in and i calculate the new mean. (incremental method for that is simple). How do i calculate the new standard deviation. The formula you gave me requires me to read the data items once and at the end of the pass i will have have the standard deviation. But i need the STDDEV values at intermediate stages as well. Is it possible ?

Murtaza

Murtaza,

You know the mean and variance s² (square of the standard deviation) and the number of items in the data set n. Let

S_x = and SS_x =

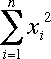
S_x is n times the mean so you can find the value of S_x as n times the mean. Once you have this value then using the expression for the variance in my earlier response

you can find

SS_x = (n-1) s² + 1/n S_x²

Now suppose you are given a new x value, x_n+1 As you remarked you can find the sum of the x values as

newS_x = S_x + x_n+1

and hence the new mean is

1/(n+1) newS_x

But you can also find the new SS_x by

newSS_x = SS_x + x_n+1²

and

new Variance = 1/[(n+1)n] [(n+1)newSS_x - (newS_x)²]

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.