Liquid is being poured into the top of a funnel

HOME

Math Central

Quandaries & Queries

Question from neroshan, a student:

Liquid is being poured into the top of a funnel at a steady rate of 200cm^3/s.
The funnel is in the shape of an inverted right circular cone with a radius
equal to its height. It has a small hole at the bottom where the liquid is
flowing out at a rate of 20 cm^3/s. How fast is the height of the liquid
changing when the liquid in the funnel is 15 cm deep?
At the instant when the height of the liquid is 25cm, the funnel becomes clogged
at the bottom and no more liquid flows out. How fast does the height of the
liquid change just after this occurs?

Neroshan,

I drew an illustration of the funnel and called the radius R and the height H. You know that R = H.

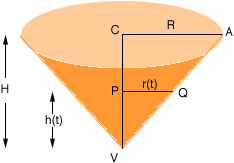
funnel

At some time t seconds the level of the liquid in the funnel is at the line segment PQ so r(t) is the radius of the surface of the liquid at that time and h(t) is the height of the liquid. Since triangles ACV and QPV are similar r(t) = h(t). Let V(t) be the volume of liquid in the funnel at that time t so

V(t) = 1/3 r(t)² h(t)

But r(t) = h(t) so this can be written

V(t) = 1/3 h(t)³

If you differentiate both sides with respect to t you will have an expression involving dV/dt, dh/dt and h(t). You know that dV/dt is a constant

dV/dt = 200 - 20 = 180 cm³/sec

So when h is either of the given values you can find the rate of change of the liquid height, dh/dt.

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.