| |||
| Math Central | Quandaries & Queries |
|
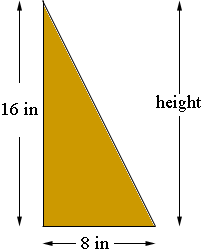
The side of a triangle is 16 inches. The base of the triangle is 8 inches. How tall is the triangle? |
We have two responses for you.
Hi,
The height can be anything from 16 inches
to a height of almost zero
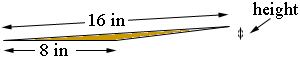
If the triangle is a right triangle as in the first diagram but it is the hypotenuse that has length 16 inches then you can use Pythagoras' theorem to find the length of the third side which, in this case, is the height.
Penny
Hi,
When looking at triangles one of the most powerful tools that we have is the Pythagorean Theorem which is a2 + b2 = c2 where a and b are the legs of a right triangle and c is the hypotenuse (side opposite the right angle). However, the only catch to the Pythagorean Theorem is that it only holds true for triangles with a right angle and our triangle does not say anything about that. In your case we are given a triangle and there is no information given to what type of triangle it is. I will assume we are talking about an isosceles triangle(a triangle that has two equal sides). So similar to your question, say we are given an isosceles triangle with a base of 10 and a side length of 13. What we can do to start out with is draw our triangle. Then once we have it drawn, drop down a perpendicular line (lines that meet at a 90 degree angle or right angle) from the peak of the triangle to the side of 10. Now what we have done is turned our isosceles triangle into two right triangles, and furthermore we have created a situation where we can use our Pythagorean Theorem. Since we are dealing with an isosceles triangle, whatever side we drop the perpendicular down to, in our case the side of length 10, the result of the perpendicular is it cuts the line in half, so our right triangle has a base of 5. Here is a diagram to help illustrate this
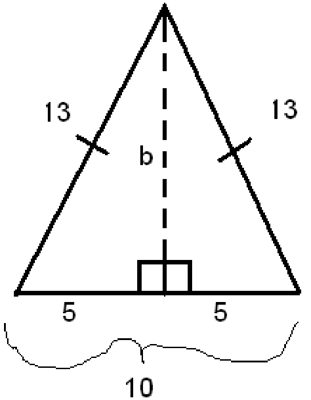
Now using the Pythagorean Theorem we can substitute in our numbers.
So, a2 + b2 = c2
52 + b2 = 13 2
The reason we put the 13 in for the c rather then the b is because the side opposite of the right angle goes in the c position, which is where 13 is located in our triangle. Then from here we can proceed to solve for b,
25 + b2 = 169
b2 = 144
√b2 = √144
b = 12
Thus the value of b is 12 so the height of the triangle is 12
Now because b is a length we do not include the value of -12, this is called the principle square root in this case.
Now if your triangle was already a right triangle, you do not have to go through the trouble of dropping down a perpendicular to make your right angle, you can just proceed with the Pythagorean Theorem and solve for side b which will be your height.
Brennan
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.