Hi Rachael,

Since the number is even it is a multiple of 2 so I can write it 2n for some positive integer n. The number cubed minus 4 times the number is then

(2n)³ - 4(2n)

I would simplify this expression and factor it to get

8n³ - 8n = 8n(n² - 1) = 8n(n - 1)(n + 1)

Thus the number is divisible by 8. Can you see why n(n - 1)(n + 1) is divisible by 6?

Penny

Hi Rachel,

I love questions like this one.

Let's start by getting a mathematical expression for "any even positive integer cubed minus four times the number". The key is to realize that if a number is even, then it can always be written as 2 times some other integer. We want to keep this bit of information with us as we proceed through the problem, so I'll write "any even positive integer" as "2k", where k can be any positive integer. So the entire expression is:

So, you need to prove that (2k)^3 - 4(2k) is divisible by 48.

This amounts to showing that [ (2k)^3 - 4(2k) ] / 48 is a whole number. We can try to factor the numerator and denominator of this expression, and hope that we can cancel common factors until we are left with a whole number expression. You can factor the expression as follows:

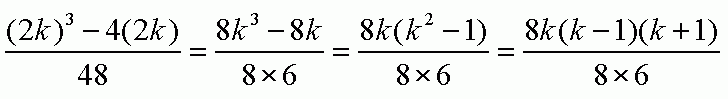
We can cancel the 8's [WHY can we do this?] and we are left with:

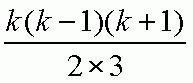
To prove that this is a whole number, you can prove that 2 will divide evenly into one of the factors in the numerator, and 3 will divide evenly into one of the other factors. I'll give you a hint: for any integer value of k, we can see that k-1, k, and k+1 are three consecutive integers. Can you show that given three consecutive (positive) integers, that 2 will have to divide one of them, and 3 another?

Haley