Hi Robby,we have three responses for you

If there are two congruent triangular bases, these must be at the top and bottom of the object. Then you need to connect the bases together, so there will be sides. A triangle has 3 sides, so there will be 3 sides to connect the bases together. Count up the vertices and faces and make sure there is the correct amount.
Now for the name. A prism is a solid with two parallel faces, called bases, that are congruent polygons. All of its other faces are parallelograms. Prisms get their names from the shapes of their bases so what is the name of this shape?

Pam

Hi Robby,

Consider what you are asking... first the 2 congruent triangular bases, thus the solid must have 2 faces which are triangles of the same shape, and these faces should be more or less parallel. Then we must have some connecting faces in between, but we are only allowed 5 faces in total, so there must be 3 more faces which connect these triangles. If we let the 3 other faces be rectangles, we can see that the condition that we have 6 vertexes is met as well, giving us a triangular (equilateral, isosceles or scalene) based prism.

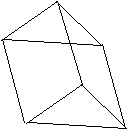
It looks like the attached picture... hope this helps!

Gabe

You can do some figuring here:

The 'hint' of the two congruent triangular 'bases' suggests these are disjoint triangles - so they involve all 6 of the vertices!

With two congruent triangles (one on the top and one of the bottom) that leaves 3 more faces to connect them. There is not much choice left now - just line up pairs of edges of the two triangles (making them coplanar) so that you only get three more faces, and fill it in.

You could make something with 6 vertices and 8 faces, if you twist one triangle relative to the other, and even try to find ones with numbers of faces in between: 6, 7 - by using non-equilateral triangles, carefully positioned!

Walter