Cut a given sphere by a plane

HOME

Math Central

Quandaries & Queries

Question from Rory, a student:

Cut a given sphere by a plane so that the volumes of the two segments formed shall be in a given ratio.
Show that in modern notation, this leads to the cubic equation
m(r+x)^2(2r-x)=n(r-x)^2(2r+x)
where r is the radius of the sphere, x is the distance of the cutting plane from the centre of the sphere, and m/n < 1 is the given ratio.
Can you help me show the solution to this question. Thank you.

Hi Rory,

I started with the circle in the plane with centre at the origin and radius r. I then sliced the circle with the line y = h, h > 0. (I am using h where you used x in your expression.) I then took the region inside the circle, above the line y = h and in the first quadrant, and revolved it about the y-axis to get a cap of the sphere.

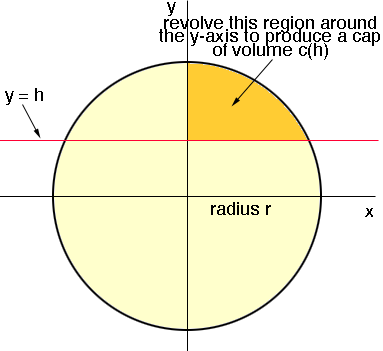
circle

I then used the method of cylindrical shells to find the volume of this cap and called the volume c(h). The volume of the remainder of the sphere is 4/3 r³ - c(h). These volumes are to be in the ratio of m to n where n > m so

m/n = c(h)/[4/3 r³ - c(h)]

I then simplified this expression and compared it to the expression you sent us, with x replaced by h.

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.