The orthcentre and the circumcentre

HOME

Math Central

Quandaries & Queries

Question from Ruby, a student:

I have tried to do this question so many times, could you please, please, please show me how to do it. I just can't get the answer:
What is the (i)Circumcentre and (ii)Orthocentre of the triangle with vertices a(-2,2) b(2,-6) c(5,3)? It would be so great if you could show me how to do this. Thanks in advance,
Ruby.

Hi Ruby,

I'll try the orthocentre and you can do the circumcentre. The orthocentre is the place where the three altitudes meet so I drew the triangle and two altitudes.

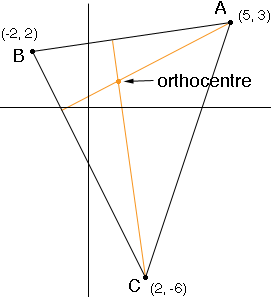
triangle

The line segment AB has slope (3 - 2)/(5 + 2) = 1/7 and hence the altitude through C has slope -7. The line through C with slope -7 is

y + 6 = -7(x - 2) or y = -7x + 8. (1)

The line segment BC has slope (-6 - 2)/(2 + 2) = -2 and hence the altitude through A has slope 1/2. The line through A with slope 1/2 is

y - 3 = 1/2(x - 5) or 2y = x + 1. (2)

I then solved the two equations (1) and (2) and found that x = y = 1. Thus the orthocentre is (1, 1).

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.