Hi Russell,

One measurement in a cone or truncated cone that can be confusing is the height. I took your measurement, 6.5 inches, as the vertical height rather than the slant height. In my diagram below the distance from E to D is the slant height of the truncated cone and the distance from A to D is the slant height of the cone.

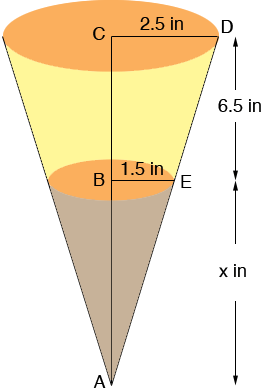
I extended d the sides of the cat food dispenser to the point A in the diagram. The length x inches is the distance from B to A. I want to find the length AD and I do it by using similar triangles and Pythagoras' theorem. (Russell you used mixed fraction notation in your question but I am using decimal fractions simple because they are easier to type.)

Triangles DCA and EBA are similar so

(x + 6.5)/2.5 = x/1.5

thus

1.5 x + 9.75 = 2.5 x, or x = 9.75 inches.

Hence the length of AC is 9.75 + 6.5 = 16.25 inches.

Triangle DCA is a right triangle so, using Pythagoras' theorem

|CA|² + |DC|² = |AD|²
16.25² + 2.5 ² = |AD|²
270.3125 = |AD|²
|AD| = 16.44 inches

In a similar fashion I found that |AE| = 9.86 inches.

Now slice along the line segment AD and roll the cone out flat to form a segment of the circle of radius
|AD| = 16.44 inches.

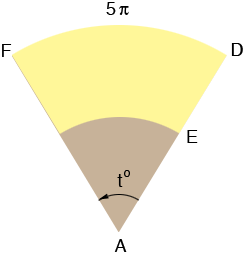
(These diagrams are not to scale.)

All that remains is to find the measure of the angle at the centre of the sector, that is t^o in the diagram.

The length of the arc DF is the circumference of the circle at the top of the cat food dispenser, that is a circle of radius
2.5 inches. Thus the length of the arc DF is 2 r = 5 inches. This length is a fraction of the circumference of the circle of radius |AD| = 16.44 inches, which is 2 16.44 = 32.88 inches. The angle measure t^o is also a fraction of the angle at the centre of the complete circle, that is 360^o. In fact these fractions are the same, that is

(5 )/(32.88 ) = t/360

Thus

t = (5/32.88) 360 = 54.7 degrees.

I hope this helps,
Penny