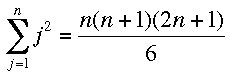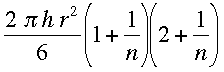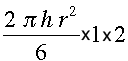Safdar,

The proper derivation involves calculus but I am going to try to convince you without the use of calculus.

A cylinder of radius r and height has volume r² h. I am going to remove the cone of radius r and height h from the cylinder and show that the volume of the remaining piece (call it S) is 2/3 r² h leaving the cone with volume
r² h - 2/3 r² h = 1/3 r² h.

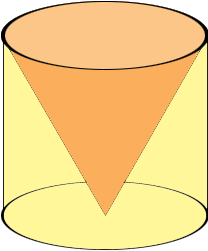
I am going to form this solid shape as a volume of revolution, that is I am going to take the triangle in the diagram below and revolve it around the Y-axis to form the shape.

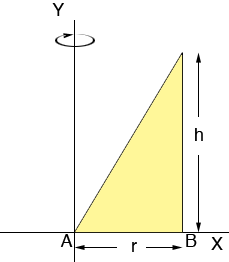
Let n be a positive integer and subdivide the interval AB into n subintervals of length r/n. The division points then will be at

1 r/n, 2 r/n, 3 r/n, ..., n r/n

Above each subinterval construct a strip of the triangle. There is one such strip in the diagram below.

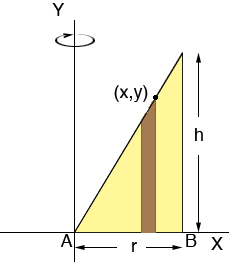
When the triangle is revolved around the Y-axis to form the solid S each of these strips will form a cylindrical shell and S itself can be seen as a collection of these shells, fit inside each other much like a child's stacking toy. These shells are not exactly cylinders as the tops are not horizontal but eventually I want to make these shells extremely thin and this discrepancy will become very small. Below is one of the cylindrical shells.

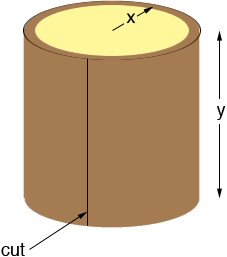
The radius of the shell is approximately x, the height is approximately y and the thickness is r/n. I can approximate the volume of the shell if I cut it along the line shown and roll it out flat to form what is approximately a rectangular slab.

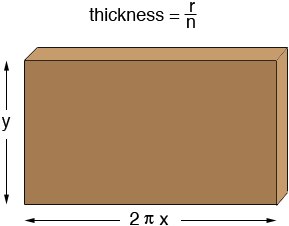
The volume of this slab is approximately 2 x y ^r/_n.

Now look back at the diagram of the triangle.

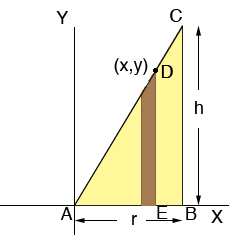
Since x is one of the division points x = j r/n for some j between 1 and n. Also triangles ABC and AED are similar so
r/h = x/y. Hence y = xh/r. Substituting these values for x and y into the expression for the volume of the slab above gives

volume of the cylindrical shell =

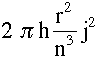
The volume of the solid shape S is then approximately the sum of these terms for j = 1 to n. Now I need the fact that

There are a number of proofs of this including proof by induction. Substitution of this expression and some simplification gives the volume of the solid S to be approximately

Finally I can improve the approximation by letting n be very large so that the vertical strips are extremely narrow. As n gets very large 1/n gets close to zero and the expression above becomes

which simplifies to 2/3 r² h.

Penny