Hi Sarah,

I reproduced your diagram and added some lines and labels.

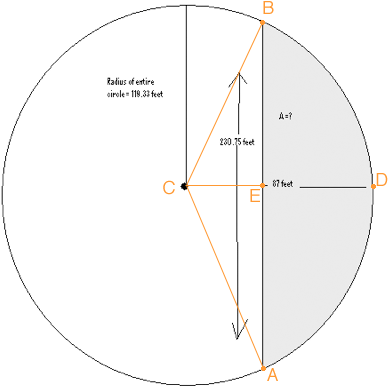
You want to find the area of the region you shaded gray in your diagram. I will show you how to find half the area and then you can double it. I am going to find the area of EDB as the area of the sector BCD minus the area of the triangle BCE.

The length of BE is 230.75/2 = 115.375 ft and the length of CE is 119.32 - 87 = 32.32 ft. Hence you can find the area of the triangle BCE using the fact that the area of a triangle is half the base times the height.

All that remains is to find the area of the sector BCD. To determine this area I need the measure of the angle BCD. Tan(∠BCD) = |BE|/|CE| = 115.375/ 32.32 = 3.5698 and hence

∠BCD = tan^-1(3.5698) = 74.35^o.

The sector BCD is a fraction of the entire circle (π r²) and the angle BCD is a fraction of 360^o. By the symmetry these fractions are the same, that is

area(sector BCD)/ (π 119.32² ) = 74.35^o/360^o

Solve for the area of the sector BCD.

Penny