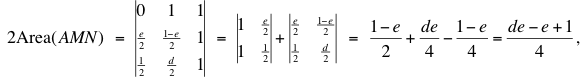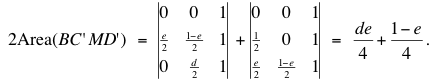A geometry problem - Math Central

HOME

Math Central

Quandaries & Queries

Question from Shamik, a student:

ABC is any triangle and D and E are 2 points on AB and AC, respectively. M
is the mid-point of BE and N is the mid-point of CD. Prove that the area of
the triangle (AMN) is 1/4 of that of the quadrilateral(BCED).

Use plane-geometry without using co-ordinates to find the solution.

My Work Done:

This can be achieved if I use analytical geometry with the help of
co-ordinates. But, I started doing it by using 'plane geometry' tricks as
specified in the problem. My work follow:

A' ? midpoint of BC
B' ? midpoint of CA
C' ? midpoint of AB
The locus of the point M is along A'C' as E moves from C to A.
The locus of the point N is along A'B' as D moves from B to A.

A'N = (1/2)*BD
A'M = (1/2)*CE

I thought a lot in the above lines but couldn't meet the solution. I have
got an intuitive solution if I could attain the following.

If I could consider one more mid-point somewhere in the diagram. If I could
split the triangle(AMN) into parts such that it can be made equal to some
quadrilateral which is 1/4 of DBCE.

Thanks

Chris responded with a proof that uses coordinates and then Shamik produced his own proof. We have Shamik's proof first and then Chris'.

Please, refer to the figure. Here is the solution.

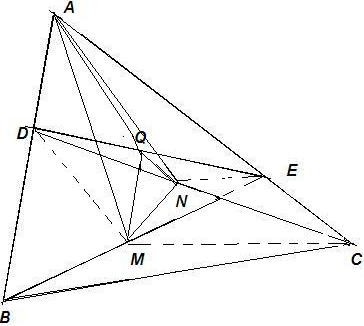
diagram

Let Q be the midpoint of DE. Join QA, QM, QN, MD, MC and NE.

Triangle (AMN) = Triangle (AMQ) + Triangle (QMN) + Triangle (QNA)

Q, M and N are midpoints of DE, BE and CD, respectively. Therefore, QM is parallel to AB and QN is parallel to AC.

And, hence, Triangle (AQM) = Triangle (DQM) and Triangle (AQN) = Triangle (EQN)

So, Triangle (AMN) = Triangle (AQM) + Triangle (QMN) + Triangle (QNA)

= Triangle (DQM) + Triangle (QMN) + Triangle (EQN)

Thus, Triangle (AMN) = Quadrilateral (DMNE) ………………. (1)

M is the midpoint of BE and so Triangle (DME) = (1/2)* Triangle (BDE) while Triangle (CME) = (1/2)* Triangle (BCE)

è Triangle (DME) + Triangle (CME) = (½)*{Triangle (BDE) + Triangle (BCE))

è Quadrilateral (DMCE) = (1/2)*Quadrilateral (DBCE)

Similarly, Quadrilateral (DMNE) = (1/2)*{Quadrilateral (DMCE)} = (1/4)*{Quadrilateral (DBCE)} ……. (2)

From (1) and (2) we get, Triangle (AMN) = (1/4)*{Quadrilateral (DBCE)}

Shamik

Chris' proof

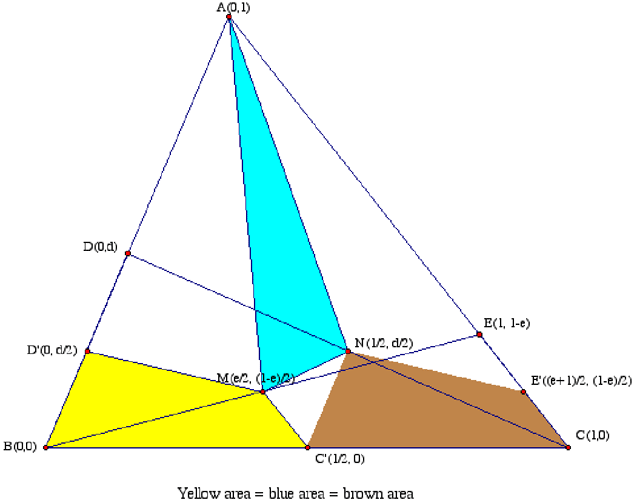
We simplified the problem a bit by first shrinking the quadrilateral BCED by ½: Take C' and D' the midpoints of BC and BD, then show that (AMN) = Area(BC'MD'). Using the coordinates shown in the figure, we compute

and

Was your argument this easy? We will let you know if we find a simple argument that avoids coordinates.

diagram

Chris

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.