Hi Stephanie,

First consider the cone without the claws so the cone is 8 mm long. We will worry about the claws later.

I am not sure what measurement you are calling the length. Is it h or s? h is called the height and s the slant height.

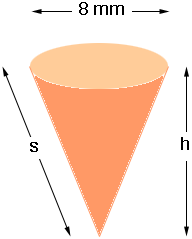
I am going to assume that the h= 8 mm.

If you slice up the side of the cone and roll it out flat you have a sector of a circle of radius s mm.

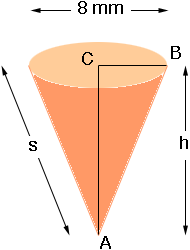
Triangle ABC is a right triangle and Pythagoras' theorem then tell us that

|AB|² = |BC|² + |CA|²

thus

s² = 4² + 8² or s = 4 √5 mm

Thus the distance |AP| = 4 √5 mm and the arc from P to Q is the circumference of the circle at the top of the cone which is 2 r = 8 mm.

We need the angle at A which is a fraction of 360 degrees. The length of the arc PQ is also a fraction of the circumference of the entire circle of radius 4 √5 mm. This circumference 2 r = 8 √5 mm. From the symmetry these fractions are the same which means

(angle at A)/360 = 8/(8 √5)

thus

the angle at A measures 360/√5 = 161 degrees.

Draw a circle of radius 4 √5 = 8.9 mm and mark off a sector with the central angle 161 degrees. Draw another circle of radius 8.9 + 3 = 11.9 mm with the same centre.

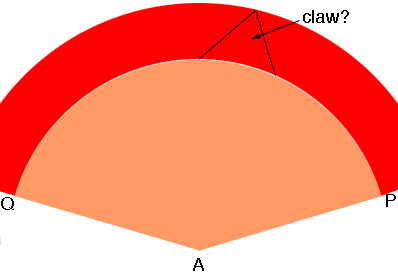
Cut the claws from the band between the two circles and roll it up to form the cone and the claws will be 3 mm long.

Penny