| |||
| Math Central | Quandaries & Queries |
|
Question from sugar, a student: A ship starts from point o sail eastward for 6 hours. Then changes its course to N50E for 8 hours and then N62W for 10 hours until it reaches the point c. If the speed of the ship was i mi/hr, what is the bearing of the side oc? |
Hi Sugar,
Her is my diagram (not to scale).
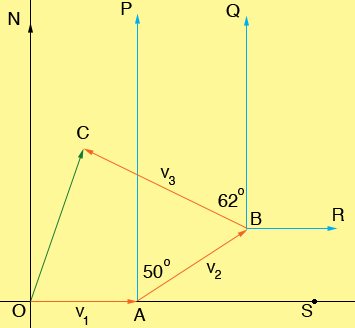
The sails from O to A then from A to B and finally from B to C. I am going to use vectors to show you one way to approach this problem.
On the first leg of the trip the ship travels at i mi/hr for 6 hours and hence it goes 6i miles. Thus the vector v1 is given by
v1 = (6i, 0)
On the second leg of the trip the ship travels for 8 hours and hence it goes 8i miles. Thus the length of the line segment AB is 8i miles. The angle BAS has measure 90 - 50 = 40 degrees and hence the vector v2 is given by
v2 = (8i cos(40), 8i sin(40))
Thus the vector from O to B is given by
v1 + v2 = (6i, 0) + (8i cos(40), 8i sin(40)) = (6i + 8i cos(40), 8i sin(40))
On the last leg of the trip the ship travels for 10 hours and hence the distance from B to C is 10i miles. The angle RBC has measure 90 + 62 = 152 degrees and thus you can use the sine and cosine function again to find the vector v3. The vector from O to C is then v1 + v2 + v3. This gives the coordinates of C from which you can calculate the bearing of OC.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.