Hi Suud,

To find the determinant of a matrix, you can expand along a row or column. Suppose we were to expand along the first row. Then we would multiply each of the coefficients in the first row by the 'left over' part of the determinant after we block out the row and the column containing that coefficient. (In the picture below, you can see that after blocking out the row and column that b is in, the leftover blue part shows the determinant we multiply b by in the expansion.) If you use this method for expanding the determinant, you must alternate signs in the expansion: the first term will have a + sign in front of the coefficient, the second will have a - sign in front of the coefficient, and so on. For example, in the matrix below, I expanded along the first row. The resulting expansion now contains several 3x3 determinants, instead of the 4x4 determinant we started with. If we now expand each of the 3x3 determinants, we can reduce them to expressions involving 2x2 determinants, which we can immediately evaluate.

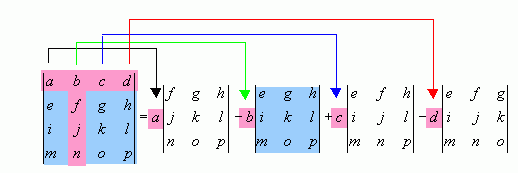
This can be a long a tedious process, but there are ways to reduce the number of calculations you have to do. There are some 'elementary row operations' that you can perform on matrices that do not change the determinant of the matrix. You can try to do some of these operations so that you end up with a row or column that has zeros in it. Then, if you expand by this row or column, you end up multiplying some of the terms by 0, so they disappear from your expression. This means you have far fewer determinants to calculate.

Getting back to your determinant, I can see that the first and fourth rows have 2 of the same entry. One of the valid row operations you can do to a matrix that doesn't alter the determinant is to subtract one row from another. I'll subtract the fourth row from the first row:

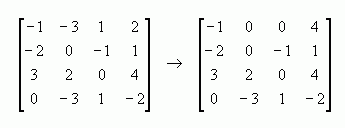
Now, I'll show you how to expand along the first row:

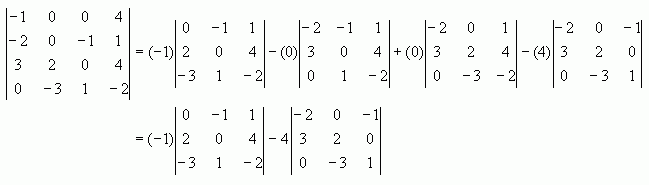
Now you can apply the same process to each of the two 3x3 determinants. Can you take it from here?

-Haley