Hi Taylor

Here is the diagram you sent and your work.

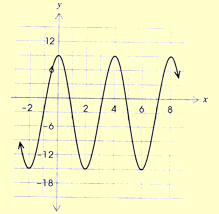
Cosine:
y=A cos B(x + C) +D
A= amplitude
Max-min /2
l 9-(-15) l /2
24/2
=12
B= period
4=2/ lBl
lBl=2/ 4
lBl=/ 2

C= phase shift
I am unsure how to do this one???

D: Vertical displacement
Amplitude+ minimum
= 12+ (-15)
=-3

12cos/ 2 (x+ Phase shift) -3

 

Sin:
y=A sin B(x+C) +D
A= 12
B= / 2
C=90
D=-3

Therefore:
12 sin/ 2 (x+90) -3

Two points:

1. The phase shift corresponds to the amount you need to shift the diagram right or left to move it to normal position (normal position would be y = cos x and y = sin x). Since your graph intercepts the y
   axis at its maximum, C is 0 for the cos function. The function is 0 at x = -1, that's where it looks like a sine wave starts. So to move it to the origin where it normally would be, you have to add 1. So the phase shift C is 1 for the sin function.
   
   
2. You came up with 90 for the sin's phase shift. As I described above it is actually 1. But your value suggests that you are mixing up degrees and radians. When you use the calculation for the period
   based on 2(pi), you are using radians. So you shouldn't use degrees for the phase shift. Both need to be done in degrees or both need to be done in radians.

A final note: When you come up with your answer to questions like this, test them. Put values of x into both functions and make sure you get back the same y value and it is the y value on the graph. If not, look for your error.

Hope this helps,
Stephen La Rocque.