Hi Tim,

The value of a trigonometric function of an angle over 90 degrees (or less than zero degrees) is not always the same as the value of its reference angle, but they can be easily evaluated. Since any trigonometric function can be written in terms of the sine and cosine functions I am going to deal wit these functions only.

Suppose you want the sine and cosine of an angle t which is between 0 and 90 degrees. Draw a circle with centre at the origin and radius 1. Draw a line segment starting at the origin and at an angle of t degrees, measured counterclockwise from the x-axis. Let this line segment intersect the circle at the point B as in the diagram. Give B the coordinates (x, y).

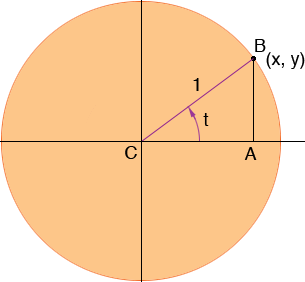
From the diagram

cos(t) = |CA|/|BC| = |CA| = x and
sin(t) = |AB|/|BC| = |AB| = y.

This illustrates the way that the sine and cosine function are defined for all angles t.

For any number t draw a lie segment starting at the origin and at an angle of t degrees, measured counterclockwise from the x-axis. Let B with coordinates (x, y) be the point where this line segment intersects the circle with radius one. Define

cos(t) = x and
sin(t) = y.

(If t is negative then measure t degrees clockwise from the x-axis.)

Here is an example where t is between 90 and 180 degrees. Again draw the line segment CB at an angle of t degrees measured counterclockwise for the x-axis and give B the coordinates (x, y). Then cos(t) = x and sin(t) = y.

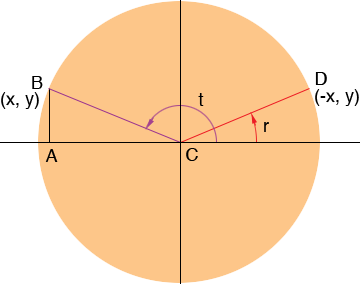
Draw in the reference angle r and the point D where the line segment at angle r degrees counterclockwise from the x-axis intersects the circle of radius 1. From the diagram, since B has coordinates (x, y), D has coordinates (-x,y). Hence

cos(t) = x = - cos(r) and
sin(t) = y = sin(r).

I hope this helps,
Penny