| |||
| Math Central | Quandaries & Queries |
|
a solid is constructed so that it has a circular base of radius r centimeters and every plane section perpendicular to a certain diameter of the base is a square, with a side of the square being a chord of the circle. find the volume of the solid at first i thought the length of a side of the square would be r, but that isn't always be true- only when the chord is in the center. so how can i solve this without any values? i don't understand the relationship between the chord and radius, except that the radius intercepts the chord at the midpoint. i know i have to take the integral to get the volume, but how do i even find the area of one of the squares? |
Hi Tricia,
I drew the base circle, the specific diameter and one chord BD that is perpendicular to the diameter and intersects the diameter at A. C is the centre of the circle and I let the distance CA be x centimeters.
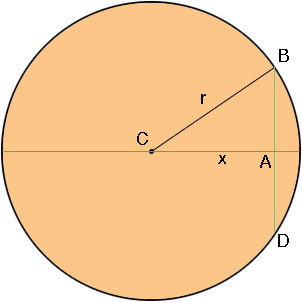
The triangle ABC is a right triangle so using Pythagoras theorem the distance from A to B is √(r2 - x2). Thus the length of the chord BD is 2 √(r2 - x2).
Does this help?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.