| |||
| Math Central | Quandaries & Queries |
|
Subject: trough - isosceles triangles the trough is 5 feet long and its vertical cross sections are inverted isosceles triangles with base 2 feet and height 3 feet. water is draining out of the trough at a rate of 2 cubic feet per minute. at any time t, let h be the depth and v be the volume of water in the trough. |
Hi Trina,
I can get you started. In my diagram the trough is part full. The surface of the water is a rectangle with length the length of the trough (5 feet) and width the the base of the inverted isosceles triangle of water at the end of the trough.
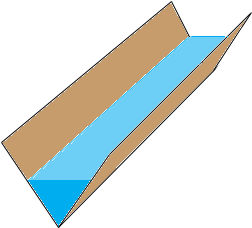
The volume of water in the trough is the area of the triangle times the length of the trough. Here is a diagram of the end of the trough with some dimensions.
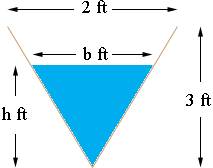
The are of the triangular face of the water is
1/2 bh
The triangular end of the trough and the triangular face of the water form similar triangles so
b/h = 2/3 of b = 2/3 h
Using this relationship you can write the area of the triangular face of the water, the volume of the water in the trough and the surface area of the water as functions of the single variable h.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.