Hi Vincent.

You didn't say anything about the pool bottom or the depth.

I'll assume the pool bottom is flat (no slope) and its depth is d feet.

The volume of water is then the depth of water (d - 1/2) times the length times the width. That gives cubic feet. If we divide by 7.48cubic feet per gallon, we get the amount of water you need in gallons (g):

g = (d-1/2) x 36 x 20 / 7.48

The amount of paint is the surface area you are going to paint divided by the amount of paint each gallon covers. The surface area you are going to paint is twice (for two coats) the surface area of the pool sides and bottom.

The bottom is length x width: 36 x 20, The sides are 36 x d, 36 x d, 20 x d and 20 x d.

Add them up and you get the surface area of the interior of the pool:

[ (36 x 20) + (36 x d) x 2 + (20 x d) x 2 ]

That simplifies to [ 720 + 112 x d ] square feet.

For two coats of paint, you are painting twice this in area. That's ]1440 + 224 x d].

Now divide by the number of square feet each gallon covers to get the number of gallons of paint you need.

[1440 + 224 x d] / 50

and finally you can multiply by the cost of each gallon to get the total cost (c):

c = 18 x [1440 + 224 x d] / 50

If your pool bottom is sloped or a more complicated shape with flat parts and sloped parts, then the calculations get more involved.

Hope this helps,
Stephen La Rocque.

Vincent wrote back.

The side view of the pool is a more complicated shape

A rectangle 4 ft by 10ft , A trapezoid unknown, and a square 15 ft by 15ft (side view shapes together) whole shape is 36 ft long Top view is a rectangle 36ft L and 20 ft W

So from the side the cross section of the pool is

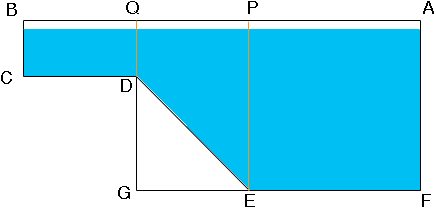
The side of the pool you need to paint is composed of a rectangle 4 ft by 10 ft, a square that is 15 ft on each side and the trapezoid PQDE. Since AB is 36 ft, AP is 15 ft and QB is 10 feet, PQ must measure 11 ft. The area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides. The parallel sides here are QD (4 ft) and PE (15 ft) and hence the area is

(4 + 15)/2 11 sq ft.

Find the areas of the rectangular piece and the square piece and add them to te area of the trapezoid to find the area of the side. Don't forget to paint the other side also.

You also have to paint the ends of the pool. At the shallow end the end of the pool is a 4 ft by 20 ft rectangle and at the shallow end the end of the pool is a 15 ft by 20 ft rectangle.

The bottom of the pool is three rectangles. The bottom of the shallow end is 10 ft by 20 ft and the bottom of the deep end is 15 ft by 20 ft. The last piece to paint is the slope. This is a rectangle 20 ft wide and its length is the distance fromD to E. But DE is the hypotenuse of a right triangle with legs GE (11 ft) and DG (11 ft) and hence you can use Pytagoras theorem to find the length of DE.

The volume of water in the pool is the cross section of the water (the region shaded blue in my diagram) times the with of the pool (20 ft.). You can find the cross sectional area as I did above for the side of the pool but you need to reduce the lengths BC, QD, PE and AF by 6 inches.

Penny