We have two responses for you.

Hi Vivienne,

If two triangles are similar then one is an enlargement of the other. This means that the corresponding angles are equal and the side lengths are in the same proportion. In the diagram below the two triangles are similar. The larger triangle has side lengths A, B and C and the smaller triangle has side lengths a, b and c.

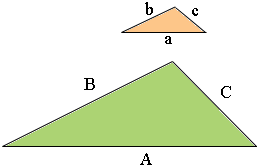
To say the side lengths are in the same proportion means

A/a = B/b = C/c

In your situation a = 17, b = 15, c = 8 and A = 51.

A/a = 51/17 = 3

and hence each side of the larger triangle is 3 times as long as the corresponding side of the smaller triangle.

Penny

Hi Vivienne.

In similar triangles, the ratios of corresponding sides are equal.

If the ratio of the shortest to longest side of the first triangle is
8:17, then that is equal to the ratio of the shortest to longest side
of any similar triangle, such as x:51.

This means 8/17 = x/51.

Can you solve the rest?
Stephen La Rocque.