A gymnast is swinging on a high bar.

Math Central

Quandaries & Queries

A gymnast is swinging on a high bar. The distance between his waist (center of mass) and the bar is 1.1 m. If his speed at the top of his swing is zero and his gain in speed is due entirely to his change in gravitational potential energy, find his speed at the bottom of his swing.

Hi William.

The gravitational force does work on the gymnast which becomes kinetic energy. This work is conserved. Therefore you can equate the loss in gravitational potential energy to the kinetic energy of the gymnast at the bottom of the loop.

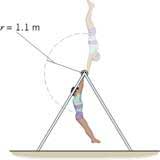
gymnast

His gravitational potential energy change is mgh, where g is the gravitational acceleration on earth (presumably!), h is the change in height of his center of mass and m is the gymnast's mass.

His kinetic energy at the bottom of the loop is (1/2)mv². As described in the problem, all the GPE was transformed into kinetic motion, so:

mgh = (1/2)mv²

Can you solve for v and substitute the known values for g and h to get the velocity?

Stephen La Rocque.>

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.