| |||
| Math Central | Quandaries & Queries |
|
Question from William, a student: Hello, A jet moving at 500.0 km/h due east moves into a region where the wind is blowing at 120.0 km/h in a direction 30.0 degrees north of east. What is the new velocity and direction of the aircraft relative to the ground? |
Hi William,
I drew a vector diagram to represent the velocities. For the wind I assumed that you are using the convention that the direction of the wind, 30.0 degrees north of east, means that the wind is coming from 30.0 degrees north of east. If my assumption is incorrect the diagram will change.
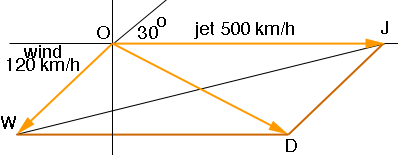
In the diagram the vector OD is the sum of the vectors OJ and OW so it represents the direction and speed of the aircraft relative to the ground.
The task is to find the length of the line segment OD and the angle JOD. For this you need to use the law of sines and the law of cosines. Since OJ and WD are parallel, the measure of angle OWD is 30 degrees. Also the length of the line segment WD is 500 and hence you can use the law of cosines to find the length of OD. Once you find this length you can use the law of sines to find the measure of the angle WDO which is congruent to the angle JOD.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.