Hi Harold,

You sent us you solution

System A (4, 2/3)
2x-3y=6 and x-3y=2
- 2 (x-3y) =2 (- 2)
-2x + 6y = - 4
2x - 3y = 6
-2x + 6y = - 4
3y = 2
y = 2/3
2x-3(2/3)=6
2x-2= 6
+2 +2
2x = 8
x = 4

which is method I would have used also. Then you asked

Could i have found the answer using the graphing method?

I sketched a graph of each equation using the intercepts. So for the equation 2x - 3y = 6 I used the points (0, -2) and (3, 0) and for the equation x - 3y = 2 I used (0, -2/3) and (2, 0).

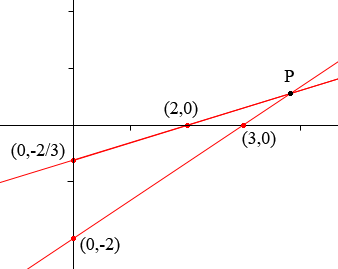
I put marks at the integer points on the axes and you can see that the x-coordinate of the intersection point P on my graph is close to 4 but not exactly 4. The problem arises from trying to place the point (0, -2/3) where the y-coordinate is a fraction. I might have been better for the line x -3y = 2 to use the points (2, 0) and (5, 1). Even then I doubt that the graph would allow me to conclude that the y-coordinate of P is 2/3.

I am not at all downplaying the use of the graphical method but I use it most often to give an estimate of the answer or a confirmation of the answer obtained by an algebraic technique. Even in my rough graph above I can see that the x-coordinate of P is approximately 4 and the y-coordinate is between 1/2 and 1. Hence I have some confidence that the solution (4, 2/3) is correct.

Penny