| |||
| Math Central | Quandaries & Queries |
|
Subject: Splitting A Circle Evenly I'm trying to make a game board and instead of having it square, I would like to give it a curve (the game is Parcheesi). The attached diagram is pretty much completed (done in AutoCAD). What I would like to know is how to manually find the points that intersect the red line. In other words, evenly split the semi-circle into 8 pieces. I know that I can do 90 degrees divided by 8 to get 11.25 degrees...but I would rather not use a protractor. How far do I measure on each red line to trace a line through it (I'm assuming that I would use the center of the "inside" circle and draw a straight line through it and some point on the red line). If it makes it easier...you can give me the measurements on the blue lines and then I would just draw a straight line between those two points. And just to describe the diagram a little more...the arcs all have a radius of 3 3/8". The outside edge of the board is actually the same circle as the "inside" arc. The "outer" arc is the same radius, but it's center is moved 1 3/4" left and up. Each rectangular block is 1 3/4" by 7/8". Oh and the drawing is not necessarily to scale. Hopefully that makes sense. Joe |
Hi Joe,
I reflected the diagram you sent in the vertical axis as I want to work in the first quadrant. I hen put a coordinate system on the plane with the origin at the centre, O, of the circle. I added some lines and labels. All my additions are in green.
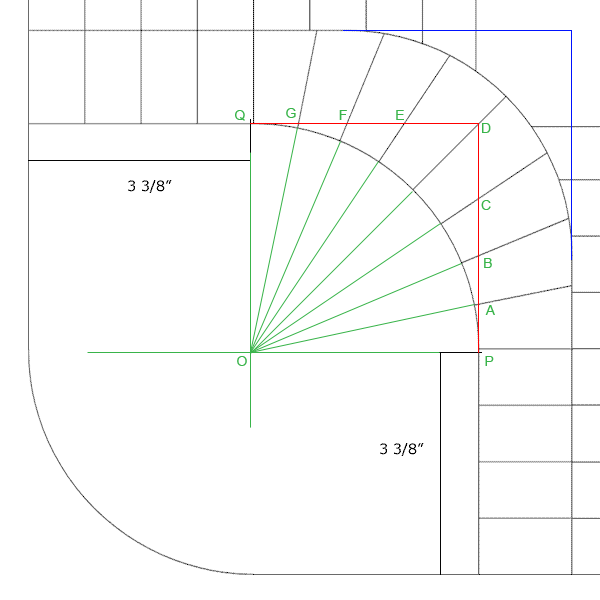
By the symmetry if you know the y-coordinates of A, B and C then you know the x-coordinates of G, F and E. I will show you how to find the coordinates of the points A.
As you stated in the problem the angle AOP is 11.25 degrees and hence the slope of the line OA is tan(11.25). Thus the equation of the line OA is
y = tan(11.25) x or y = 0.1989 x
The x-coordinate of A is 3 3/8 = 3.375 inches and hence the y-coordinate of A is
y = 0.1989
3.375 = 0.67"
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.