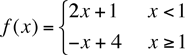Subject: Piecewise Functions
Name: Kait
Who are you: Student

OK,so I am very confused and am hoping that you can help. I am involved in Direct Link,which is a program for students who are too sick to actually go to school. They do their classes over the phone and its really hard to learn math that way. We discussed how to graph piecewise functions today and I'm very lost!! I'm sitting here staring at this problem that says:
f(x){2x+1, if x <1
f(x){-x+4, if x is greater than or equal to 1.

please help!!

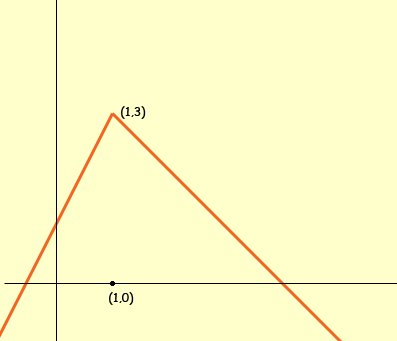
Hi Kait,

I agree that math is hard to communicate over the phone or even in ordinary text. That is why we decided to use the web to post answers to questions sent to Quandaries and Queries, that way we can include diagrams and mathematical notation.

You have a function defined in two pieces, one piece if x < 1 and another is x ≥ 1.
For x < 1 the expression is

f(x) = 2x + 1

and for x ≥ 1 the expression is

f(x) = -x + 4

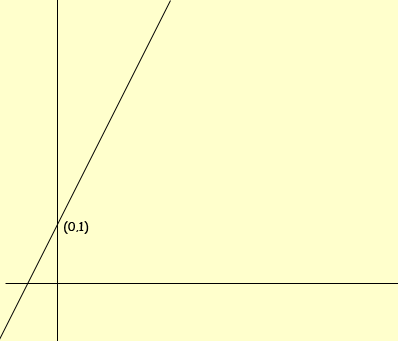
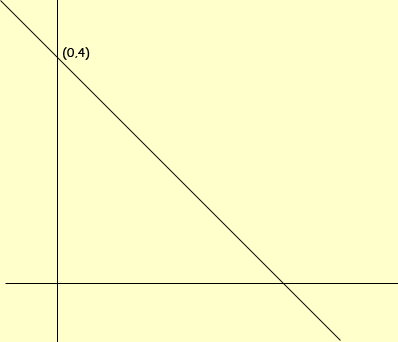
I would first make a sketch of the graphs of these two expressions, ignoring the restrictions on x. Both of these are straightforward to plot since the equations are in the slope-intercept form.

f(x) = 2x + 1

f(x) = -x + 4

But now I only want the piece of the first graph for x < 1

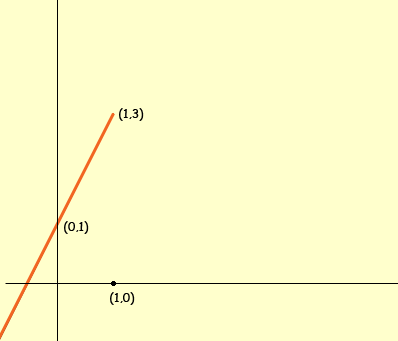
f(x) = 2x + 1, x < 1

and the second graph for x ≥ 1.

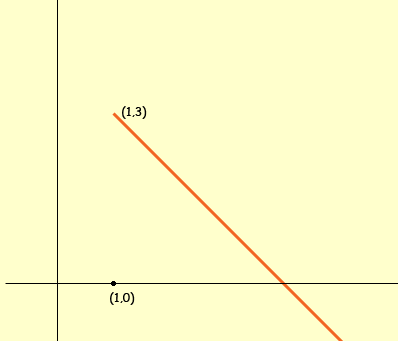
f(x) = -x + 4, x ≥ 1

Finally put these two pieces together to form one graph

Notice that these two functions f(x) = 2x + 1 and f(x) = -x + 4 link together at x = 1 since they each have the value of 3 at x = 1. this certainly doesn't need to happen with functions defined in a piecewise fashion.

I hope this helps,
Penny