How many cubic yards of cement will be required to fill a hexagonal concrete form with equal 12 foot sides that will be 3 feet thick?

My name is Lewis
I am a homeowner

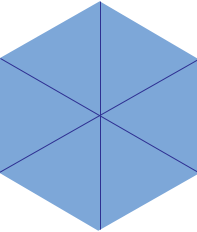
Hi Lewis,

I am going to look at a hexagon with side length L units. If you join each vertex of a hexagon to the centre you can see that the hexagon can be divided into 6 congruent, equilateral triangles.

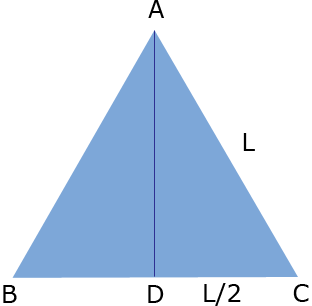
Now look at one of te triangles and label its vertices A, B and C.

D is the midpoint of BC and triangle ADC is a right triangle, so using Pythagoras theorem we get

L² = (L/2)² + |AD|²

and hence

|AD|² = (3 L²) /4

and thus

|AD| = (√3 L) /2

Thus the area of the triangle ABC is

(half the base) height = (L/2) (√3 L) /2 = (√3 L²) /4

The hexagon is composed of 6 of these triangles so 6 times the triangle area gives

hexagon area = ( ^{3 √3}/2) L² square units

The volume of your hexagonal slab is the area of the hexagon times the thickness. Since you want the volume in cubic yards you need to change the dimensions to yards before you calculate the volume. There are 3 feet in a yard so your form is 4 yards on the side and 1 yard deep. Thus the volume is

(^{3 √3}/2) 4² 1 = 41.6 cubic yards.

Penny