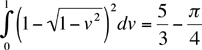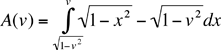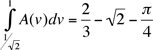Subject: geometry
Name: Liz
Who are you: Teacher

What is the volume of the solid remaining if a unit cube has a hole drilled thru one face to the opposite side and the hole that is drilled is a cylinder of unit diameter. Then the cube is rotated and an identical hole is drilled from an untouched face to the opposite side. Then the cube is rotated and an identical hole is drilled between the last two untouched faces. This will result in the cube vertices and the remaining volume of the cube falling into 8 parts. What is the total volume of these 8 parts. How is this volume calculated?
Thanks so much. I have been thinking about this for a while and cannot find an answer. I have never met anyone who can answer it and I have asked lots of math teachers.
Best regards,
Liz

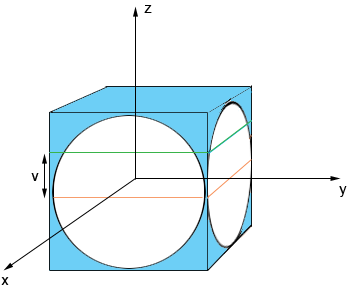
Hi Liz ,

I changed the cube to have dimensions 2 by 2 by 2 so that the holes are circular with a radius of 1 unit, that makes the numbers simpler. I put the centre of the cube at the origin with the z-axis is upwards. Drill a hole centered along the x-axis and and a second centered along the y-axis. The orange lines are in the xy plane. (My diagram is not great but I hope you see what I am doing.)

Slice through the cube by a plane parallel to the xy plane, v units above the xy plane (at the the green line). Lift off the piece above the slice and look down from the top. You see

The white parts are removed and only the blue remains. I am not going to show you the details but the lengths of the sides of each of the squares is

1 - Sqrt[1 - v²] where Sqrt is the square root.

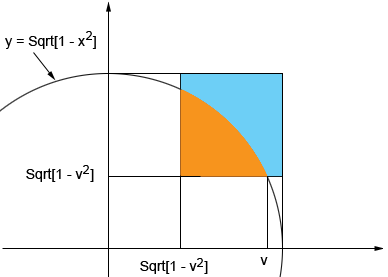
I want to focus on the part of the cube with x, y and z all positive that remains after drilling these two holes. The volume of this solid is

Now drill down from the top. One of two things happen.

If v is small, less than ¹/_√2 then the drill misses the blue part that remains after the first two holes were drilled.

If v is larger than ¹/_√2 then you see

and the orange pieces are removed by the drill.

Let's look more closely at one of these regions.

Let A(v) be the area of the orange bite removed by the drill then

The volume of the region with x, y and z positive that remains after drilling the first two holes and is subsequently removed by drilling the third hole is

Thus the volume that remains after drilling the three holes in my 2 by 2 by 2 cube is

8 (1 - √2 - ^3π/₄) 

Penny