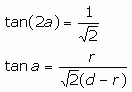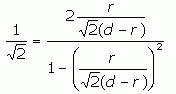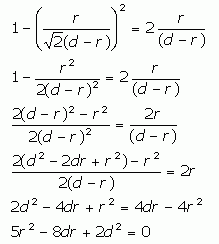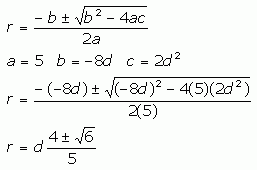 |
 |
|
Subject: Geometry Given a cube and a cross diagonal, what is the largest size sphere that fits in the cube and does not touch or intersect the cross diagonal?
|
|
I would suggest 'making a model' at least on the computer, to see what can happen. If you have an expanding sphere it will stop when it hits an face, and this diagonal. If you imagine it, you can see that it will be able to slide along till it hits two, then three faces. So the short form is it should touch three faces around some corner. If you look down the diagonal, you will see that the entire cube has a three-fold rotational symmetry around the diagonal. Moreover there is a 'central symmetry' that reverses the the two ends of the diagonal, and which reverses the three vertices visible from the 'top' (all equivalent under the rotation) and the three vertices on the bottom. In short, all six of the corners which are not on the diagonal, are actually equivalent (a sphere in one will fit in the other five). So pick one of these corners, and blow the sphere up from this corner until it hits the diagonal. I have not provided the exact numbers - but where to find one that touches the diagonal and is a maximum. By the way, if you insist it does not touch the diagonal, then there is no 'largest sphere' but an upper bound which does touch, and a sequence of slightly smaller spheres which approach this. Walter Whiteley Hi there. First let us thank you for a very entertaining geometry problem! To begin, let's consider the cube first. We'll draw the cube's diagonal in red, the bottom diagonal in blue and the frame of the cube in black:
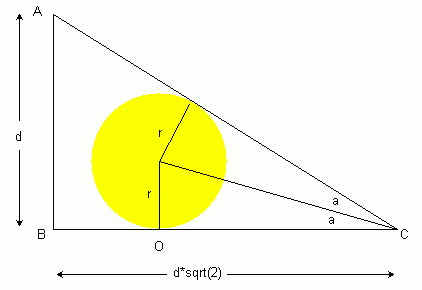
As you can see, the largest sphere that fits under the red line will be the one that touches the three walls of the cube (in other words, the sphere is pressed into the corner at B. It doesn't touch the line AB, but its cross-section as a circle has to fit inside the triangle ABC. Let's call the distance from A to B (the side length of the cube) d. Since BC is the hypotenuse of the right-isoceles triangle whose legs are both d units, the distance BC is d√2.
Now let's see a view from the bottom (the face that includes the line BC. We'll label the radius r, the point the circle touches a wall W and the point the circle touches the bottom face O:
This gives us enough information to flesh out a diagram of triangle ABC now:
Using trigonometry, the tangent of angle ACB equals the opposite side (length d) over the adjacent side (length d√2). So tan ACB = 1/√2. Note that we've shown angle ABC divided in two. The lengths from the two points of tangency to C must be equal due to circle geometry. That in turn means we have two congruent triangles, so angle ACB can be divided in two. We've labelled each half as a. So we can rewrite tan ACB as tan (2a). However, we also know that tan a is r divided by the length of OC. Since BC is d√2 and BO is r√2, OC is √2(d-c). So we have two equations with tangent:
There is a trigonometric identity that says:
In our case, this means:
So when we substitute in our expression for tan a, we get:
From here on, it is just algebra. I'll show the steps so other readers can learn:
Now we can use the quadratic formula to find the value of r in terms of d. However, this gives us two values for r. With a plus sign, though, r is bigger than d, which doesn't logically fit your description, so we are left with the minus:
which is in the neighbourhood of 0.31d. This was fun!
|
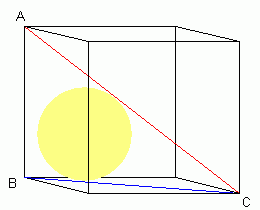The corners of a right-triangle are labelled A, B and C.
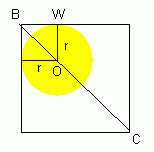Notice that triangle BOW is a right-isoceles triangle with the two legs having sides of r. By using the pythagorean theorem, the length from B to O is r√2.
 |
 |
 |