|
Hi Melenie,
Before reading Sue's description below of the process she uses to find the LCM I want to show you a problem that came from a woman I know who teachs at the First Nations University of Canada. In Canada many of the aboriginal people call themselves First Nations People. She is an artist who teaches traditional bead work and quill work. She told me that she gives her students this type of problem before they start designing a bracelet.
The First Nations people of the Plains decorated clothing, bags, containers, quivers, and many other items. Beading was not only decorative, but symbolic and spiritual as well. For example, certain colours and shapes have symbolic meanings, but the beadwork could also have a personal meaning. Many of the patterns we see today are based on quillwork designs used before the introduction of glass beads (by European traders).
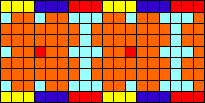
Flora is designing a bead bracelet in the above pattern. The flower pattern repeats every eight beads. The border pattern repeats every nine beads. If she needs the bracelet to be between 60 and 100 beads in length in order to fit her wrist, how many beads long should she make it so that the bracelet ends at a point where both patterns are complete?
The answer is the LCM of 8 and 9 and these specific numbers make it quite straightforward to solve, but Sue's method will work for larger numbers.
Penny
Hi Melenie.
There are three steps I usually use:
- Factor each of the numbers into its prime factors
- Find out which factors are common to both numbers.
- Multiply one copy of the common factors by the uncommon factors.
Here's an example in detail. Find the LCM of 225 and 180.
- Factor 255. What goes into 225? 5 does: 5 x 45. Nothing but 1 and 5 go into 5, so ignore it for now. Factor 45. It is 5 x 9. again nothing goes into this five, but the 9 is 3 x 3. So 225 = 5 x 5 x 3 x 3. Now factor 180. It is 2 x 90. and 90 is 2 x 45. and 45 is 5 x 9. and 9 is 3 x 3. So 180 = 2 x 2 x 5 x 3 x 3.
- We have 5 x 5 x 3 x 3 and 2 x 2 x 5 x 3 x 3. Common factors are 5, 3 and 3 (both numbers have two threes and at least one 5). Uncommon factors those left over after you cross off the common factors from each. So the set of factors just has a 5 left and the second set has 2 and 2 left.
-
The common factors are 5, 3, 3 and the uncommon factors are 5, 2, 2. So multiply them together: 5 x 3 x 3 x 5 x 2 x 2 = 900.
That means that the lowest common multiple of the original two numbers 225 and 180 is 900.
There are some shortcuts to this approach, but it's best not to complicate things more than necessary and this method will always work for you.
Stephen La Rocque.>
|





