y = x^2

HOME

Math Central

Quandaries & Queries

Subject: Graphing quadratic equations
Name: Mike
Who are you: Other

Graph the quadratic equation: y=Xsq-2
this does not meet the quadratic equation form of xsq + x + constant or am i just missing something in my text????
IF it is, Is it necessary to find the x axis of symmetry, in this case the x axis = 2, and then use values on either side of 2?

Or can i just use convenient values for x to solve for y so i can graph the equation?

My solution for this equation was to just use values of -2 through 2 and graph a parabola opening upward ( xsq coefficient is positive)

thanks for the help
Mike

Hi Mike,

y = x² - 2 is a quadratic equation of the form y = ax² + bx + c, let a = 1, b = 0 and c = -2.

You can certainly plot the graph by using values of x from -2 to 2 but I want to show you another way. I expect that you know the graph of y = x²

y = x^2

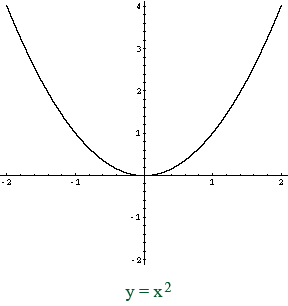
If you compare the functions y = x² and y = x² - 2, call them (1) and (2), the difference is that in (2) for each value of x the corresponding value of y is 2 less than in (1). Hence when plotting (2) the points on the graph of (1) are moved down two units.

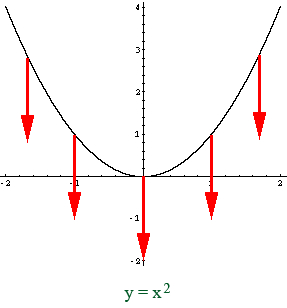
arrows

Thus the graph of y = x² - 2 is

y = x^2 - 2

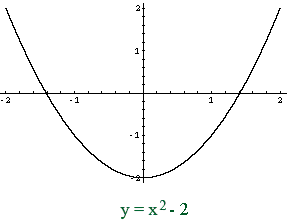
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.