 |
 |
|
Question from Namrata: AB is a diameter and AC IS A CHORD OF A CIRCLE SUCH THAT angle=30. the tangent at C intersect AB produced in a pointD. Prove that BC=BD. |
|
Hello Namrata, I tried drawing a diagram based on your description and this is the best I could do:
The first step is in recognizing that a perpendicular to any tangent of a circle must pass through the center point of the circle. As well, any diameter of a circle must pass through the center point of the circle. That means that point D must be the center of the circle. The second step is remembering the property that the measure of The third step is realizing that any line segment from the center to the circumference is a radius, so this means CD = BD. The last step is looking at triangle Hope this helps, |
 |
 |
 |
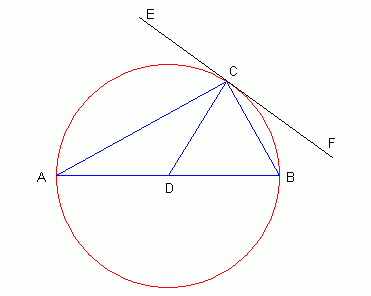 As you can see, I have drawn the tangent line to the circle at location C (I've called it the line EF). But you can see from the diagram that the tangent line EF doesn't intersect the diameter AB. I think what you meant to say was the perpendicular to the tangent at C intersects AB. That's what I've drawn, because the rest makes sense then.
As you can see, I have drawn the tangent line to the circle at location C (I've called it the line EF). But you can see from the diagram that the tangent line EF doesn't intersect the diameter AB. I think what you meant to say was the perpendicular to the tangent at C intersects AB. That's what I've drawn, because the rest makes sense then.