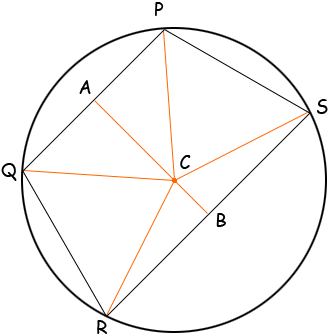
Subject: circles
Name: Namrata
Who are you: Student

If two sides of a cyclic quadrilateral are parallel, prove that
(1) remaining two sides are equal,
(2) both diagonals are equal.

Namrata,

I can get you started.

In the diagram above PQRS is a cyclic quadrilateral with PQ and RS parallel. A is the midpoint of PQ and C is the centre of the circle. Join A to C and extend AC if necessary to meet RS at B. Triangles PAC and AQC are congruent so angles PAC and CAQ are right angles. Since PQ and RS are parallel, angles CBS and RBC are also right angles. Use this fact to show that triangles CRB and SCB are congruent and thus that B is the midpoint of RS.

Can you complete the problem now?
Penny