Subject: Octagonal Stop Sign
Name: Phil
Who are you: Teacher

Hello! My colleagues and I are in a discussion about how many true "sides" an octagonal stop sign has. I say that it has 10 true sides because of the front back sides of a stop sign (3D octagon). Is this correct terminology or should the front and back "sides" be referred to as faces -- equaling 2?

Thanks!

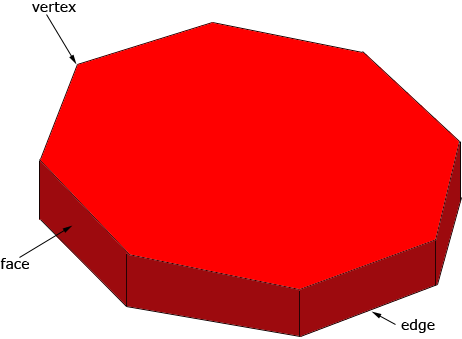
Hi Phil,

By mathematical definition, an octagon is an 8 sided 2-D shape. A stop sign, technically, is not 2-D, so it is not an octagon. A stop sign is 3-D, and has 10 faces. We could consider only the front face of a stop sign, which would be an octagon (now, we are ignoring the thickness of the sign, and it has 8 sides). It is common place to refer to a stop sign as an octagon, because it has 8 edges around it's front face - this is informal language that is fine for day-to-day communication, but is not acceptable in within the precise language of mathematics.

Paul

Hi Phil,

Phil,

I agree completely with Paul's response but I want to add something. An octagon is an 8 sided 2-D shape but in describing the 3-D "stop sign" shape (I drew one below that is thick enough that you can see the third dimension) mathematicians use the terms vertices, edges and faces.

I have always thought that they do so precisely because the term "side" carries connotations in English that give rise to exactly the ambiguities that you and your colleagues detected.

Harley

my 2 cents worth:

Technically, a "side" is not a mathematically precise term, so mathematicians avoid it. However, even we use the term "side" in the same loose way that everyone else does, so really we are looking for a bridging definition that offers more precision for the word "side" without breaking any of its conventional linguistic meanings.

I would propose that a "side" be one dimension less than the object whose side it is. For example, the side of an octagon is 1 dimension (so it is part of a line) since an octagon is a 2 dimensional shape. A side of a cube is a two-dimensional shape (part of a plane).

Curved surfaces still pose a problem and although we could continue to refine our definition, I expect shapes like the möbius strip and the Klein bottle will continue to vex us. Look these up if you are curious about why.

Stephen La Rocque.>