| |||
| Math Central | Quandaries & Queries |
|
Subject: Math/Area An octagon is inscribed in a square so that the vertices of the octagon trisect the sides of the square. The perimeter of the square is 108 centimeters. What is the number of square centimeters in the area of the octagon? This information is for my granddaughter. I am trying to help with her school work. If you could show me how to solve this problem, it would be greatly appreciated. Thanking you in advance for your cooperation. |
This is best done by three simple steps:
- the answer you want is the area of the square minus the area of four 'corner triangles' (see the diagram):
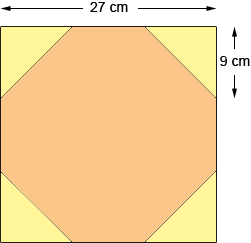
Now for the square: the four sides are each 1/4 of the perimeter (the sum of the sides): 27 centimeters.
From this you can calculate the area of the whole square.
For the triangles: the short sides are each 1/3 of the sides of the square: 9 cm.
From this, and the right angle in the corner, you can calculate the area of each of the triangles.
Alternatively, each pair of the triangles forms a square of side 9 cm.
So you now have the pieces. You can now complete the pieces and subtract.
There is a second way to check this answer:
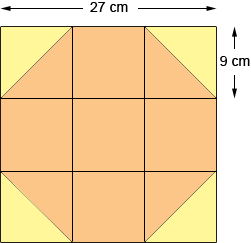
With this you can see that the whole square is divided into 9 smaller squares.
Four triangles (or two of the squares) are left out. So you want the area of seven of the squares, each of which is 9 cm by 9 cm. Again, you can complete the calculations!
Walter Whiteley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.