 |
 |
|
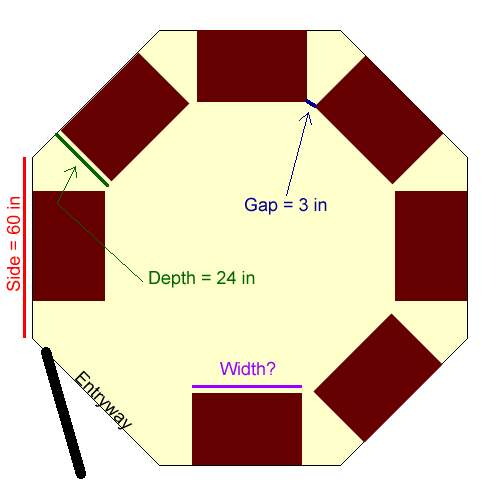
Question from Rick, a cabinet maker: I am a cabinetmaker, and I have a client who has an octagonal room which he would like to be used as a walk-in closet. Each side of the octagon is 60" in length. Each wall section is to have a 24" deep cabinet installed on it. I am trying to figure out the width of each cabinet allowing for a 3" space between cabinets at the front corner. |
|
Hi Rick. That's an interesting geometry problem you have there. I'll draw it as best I can first:
So since we know the side of each room is 60 inches, we can try try to solve for the gap between the corner of the cabinet and the corner of a room (this gap on each side of the cabinet plus the cabinet size totals 60 inches). So let's zoom in on a corner and make a geometric sketch, labelling some angles and points of interest:
Each angle in an octagon is 135 degrees, so angle s is half of that: 67.5 degrees. Since triangle ABC is a right triangle, angle t is 90 - 67.5 = 22.5 degrees. That's all we need for angles. We want the distance from D to F to be 3 inches, so DE is 1.5 inches. Due to symmetry, triangle DEC is a right triangle. We know the length of DE, so we can use sine to calculate the length CD: DC = DE / sin t = 1.5 / sin (22.5) = 3.92 inches. Now we can add that to the depth of the cabinet (24 inches) to get the total length AC: 27.92 inches. The next step is to calculate the length AB. Remember that ABC is a right triangle, we know t and we know AC, so we can now calculate AB using tangent: AB = AC tan t = 27.92 tan 22.5 = 11.56 inches. The last step, of course is simply to subtract AB from the wall width twice (once for each side of the cabinet): Width of cabinet = 60 - 2 (11.56) = 36.87 inches. Of course, all this is based on perfect walls in a perfect octagon, so you'll have to be very careful to judge the room you are working on accurately! Hope this helps,
|
 |
 |
 |
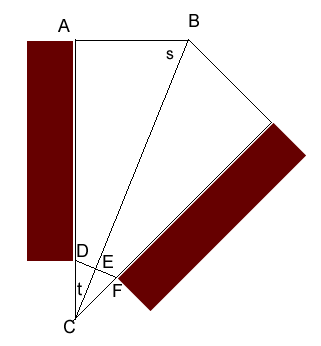 So in this diagram, we want to find the length of the side AB.
So in this diagram, we want to find the length of the side AB.