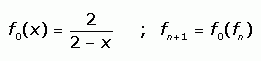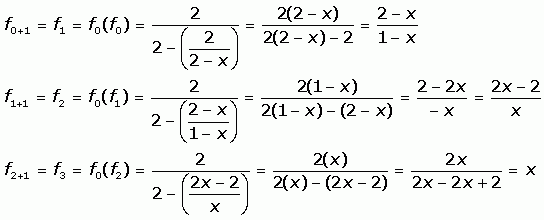Question from RJ, a high school teacher:

My son asked me this question and I am not sure about it so if you could help me solve it I would greatly appreciate it. The question is :

Let f0(x) = 2/2-x and fn+1 = f0 o fn for n greater than or equal to 0. Find a formula for
fn and prove it by mathematical induction. Recall that o represents function composition.
i.e., (f o g)(x) = f(g(x)).

Hi RJ.

Whenever you are trying to come up with a formula or whenever starting out a mathematical induction proof, it is worthwhile to try the first few values of n to see what is happening. So starting with the function definition:

Let's look at the first few values of f_n (x):

So this function cycles. The proof is almost done already, so I'll leave the rest to you.

Stephen La Rocque.>

RJ wrote back

Hi,
I understand everything you showed me in the answer, but how does that show me the proof by mathematical induction. I don’t understand, all it seems like is that you are plugging in one equation for the other. I'm still a little confused. So if you could give me a little more insight I would appreciate it.
Thanks

What Sue did was to show that

f_o(x) = 2/(2-x)
f₁(x) = (2-x)/(1-x)
f₂(x) = (2x - 2)/x and
f₃(x) = x

From here it follows that

f₄ (x) = f_o o f₃ (x) = f_o(x) = 2/(2-x) and it follows that
f₅(x) = f₁(x)
f₆(x) = f₂(x)
f₇(x) = f₃(x)

and the pattern repeats. The essence of the induction argument is to be more formal with the clause the pattern repeats.

I am going to change the indexing so that it starts at 1 rather than 0.

Let g_n = f_n-1for n = 1, 2, ... For each n there are integers k and i with i = 1, 2, 3 or 4 so that n = 4k + i. The pattern I see and want to prove is that for each k

g_4k+1(x) = 2/(2-x)
g_4k+2(x) = (2-x)/(1-x)
g_4k+3(x) = (2x - 2)/x and
g_4k+4(x) = x

I am going to prove this using induction on k. Sue proved this for k = 0. This is the first step in the induction argument. I want to show that the pattern repeats. To do this I assume that I have proved this for some particular value of k and I want to verify it is true for the next value of k. So I am assuming the 4 equations above are true for some particular value of k but not necessarily for any larger k.

Using the definition in the problem

g_4(k+1)+1(x) = g_(4k+4)+1 (x) = f₀(g_4k+4(x)) = f₀(x) = 2/(2-x)

In a similar fashion you can show that

g_4(k+1)+2(x) = (2-x)/(1-x)
g_4(k+1)+3(x) = (2x - 2)/x and
g_4(k+1)+4(x) = x

Hence the pattern does hold for k+1.

Thus, by induction the formula I found for f_n is valid for all n = 0, 1, 2, ...

Penny