Hi Aakash.

Period of a trig function

The period of a trig function t(x) is the distance in x it takes for the pattern to repeat itself.

The graph of the tangent function tan(x) looks like this (x in degrees here):

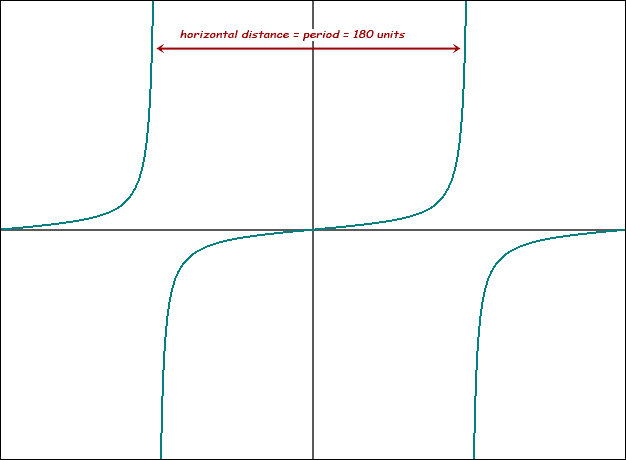
So the period in this case is 180°, since the pattern repeats every 180 units of x. If we replace x with 3x +90°, then graph tan(3x +90°), it looks like this:

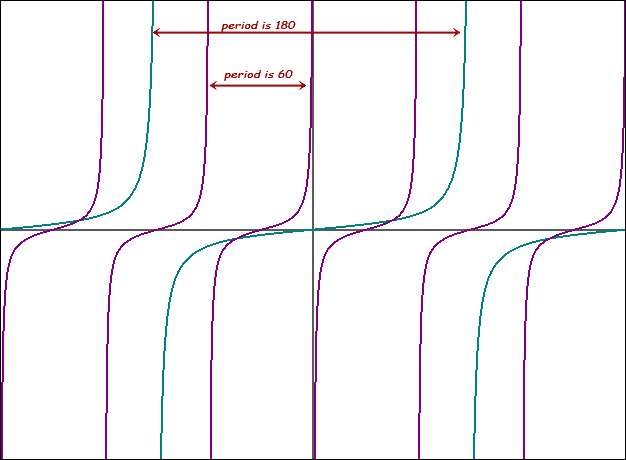
So the period of this function is 60°. In fact, that factor in front of the x tells us what the period will be, if we know what the period is normally (without a factor given). In the case of tan() it is 180°. You multiply the normal period by the reciprocal of the factor in front of x. You should be able to determine what it is normal for sine and cosine yourself.

Adding trig functions

When you add trig functions together, the overall pattern repeats when there is a whole number of all the individual periods. Say you had periods of four trig functions: 60°, 360°, 16°, and 90°. You find the lowest common multiple (LCM) of these figures to find the period of the overall function:

720° = 60° × 12 = 360° × 2 = 16° × 45 = 90° × 8. Period is 720°.

Solve your problem the same way: First find the period of each trig function, then find the LCM and you will have the overall period of the sum of the trig functions.

Hope this helps,
Stephen La Rocque.