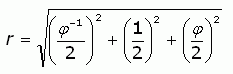Circumscribing a golden cuboid with a sphere: surface areas

HOME

Math Central

Quandaries & Queries

Question from ainslie, a student:

Please help me with this problem

A golden cuboid is defined as a rectangular prism whose lengh, width and hight are in the ratio of phi : 1 : 1/phi Prove that the ratio of the Surface Areas of the golden cuboid to that of the sphere that cicumscribes it is Phi : Pi.

thank you

Hi Ainslie.

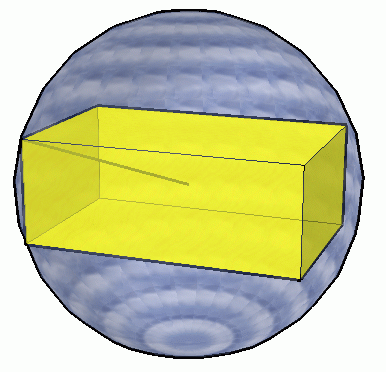
You are asked to find the ratio (call it R) of the surface area of the cuboid to that of the sphere:

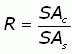
The formulas for the surface areas of the cuboid and the sphere are easy:

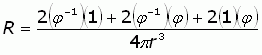
To find the surface area of the sphere, we will need to determine its radius r (you can see it represented faintly in the diagram.

Since r is also the distance from the geometric center of the golden cuboid to a corner, we can use the distance formula to find r.

Now you have all the pieces you need to assemble the solution, Ainslie. Substitute for r and simplify.

Hope this helps,
Stephen La Rocque.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.