Hi Alexander. From your description, I'm going to assume the base is a square and the top of the pyramid is directly above the center of the square. Here's a rough sketch to help out:

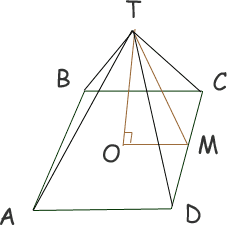It should be fairly clear from symmetry that each triangular face of the pyramid is congruent (the same size and shape). You tell us that the length CD is 0.6 m and that the length OT is 1.0 m.

Notice the right triangle TOM. I know the length of OM must be half of BC, which is 0.6 m, so OM is 0.3 m. Now we have the lengths of two sides of a right triangle, so we can calculate the length of MT, the hypotenuse by using Pythagorus' Theorem:

     MT² = 0.3² + 1.0²
     MT² = 1.09
     MT = 1.044 m

However, just looking at triangle DCT, we see that the base length is CD, which is 0.6 m, and the height of the triangle (in two dimensions) is MT, which is 1.044 m. Since the area of any triangle is ½  base  height, the area of one triangular side of this pyramid equals ½  0.6  1.044, which is 0.3132 m² .

There are four congruent triangles like this, plus the area of the square base itself (assuming you want to include that). Add them up and you have the total surface area of the pyramid structure.

Hope this helps,
Stephen La Rocque.