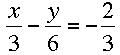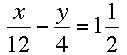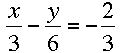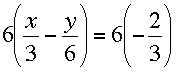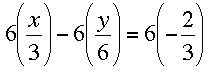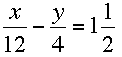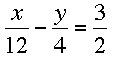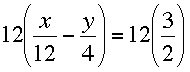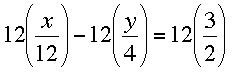Alyca,

I've re-written your question here:

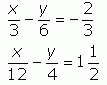
The first thing I would do is to convert any mixed fractions to improper fractions and then multiply one of the equations by some factor so that one of the terms is the negative of the corresponding term in the other equation. In this case, I'd multiply the first equation by -1/4 so that it has a -x/12 term which is the negative of the x/12 term in the second equation:

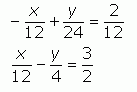
Now I can eliminate the x terms by adding corresponding sides of the equation together. I add the two left sides and the two right sides:

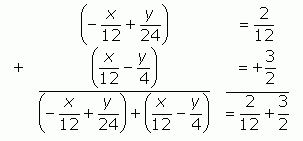
When I re-arrange this, the x terms cancel.

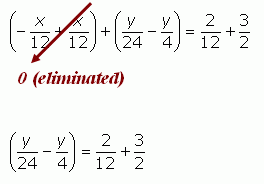
Now I can solve for y. Then I can use the value of y to find x using either of the original equations.

Hope this helps,
Stephen La Rocque.

Hi Alyca,

This is the system that you want to solve by elimination:

It can be difficult to work with equations that involve fractions, so why don’t we manipulate them to get rid of the fractions?

You should know from previous math experiences that you can do any operation to both sides of an equation and still maintain the equality.  For example, I can multiply both sides of the equation 5 = 5 by 2 to get 10 = 10.

Let’s use this property to simplify the first equation in your system:

To eliminate the fractions, we need to multiple both sides of the equation by the lowest common multiple of the denominators (3, 6, and 3) – in this case, 6.

Distributing the 6 and simplifying, we get:

As you can see, this equation is much easier to deal with than the original.

Follow the same procedure for the second equation, only start by converting the mixed number to an improper fraction:

Multiplying by the lowest common multiple of denominators, 12

Now the system of equations has been transformed into something that looks like this:

2x - y = -4

x - 3y = 18

You should be able to solve it from here.  Just apply the method of elimination to the new system and you will get your answer. 

Note:  When you check your answer in this type of question, use the original system to make sure there were no math errors made while eliminating the fractions.

 Ashley