| |||
| Math Central | Quandaries & Queries |
|
I have to find the area of the shaded region where there is an octagon inscribed in a circle The radius is 4 inches. The shaded region is everything besides the octagon inside the circle. How can I find the area of the shaded region? Thank you! |
Hi Amy.
The area of the shaded region is the area of the whole circle minus the area of the octagon:

The radius of the circle can give you the area of the octagon:
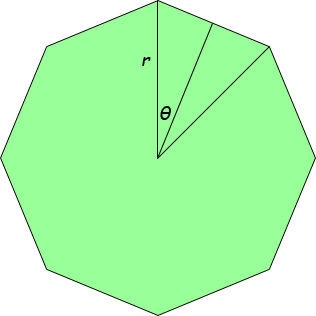
All the way around the center of the octagon is 360°, as you know. Therefore, what is the size of θ ?
Knowing θ and r, can you use sine and cosine to find the dimensions of each right triangle?
From this, you can find the area of each right triangle, multiply by 16 (2 triangles per side of the octagon) and you have the area of the octagon.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.