| |||
| Math Central | Quandaries & Queries |
|
my dad, who is a welder, asked me a question pertaining to chords and points on an arc to which I cannot for the life of me find an answer or an equation. if you could help, it would be much appreciated. Angela sent us the diagram below: 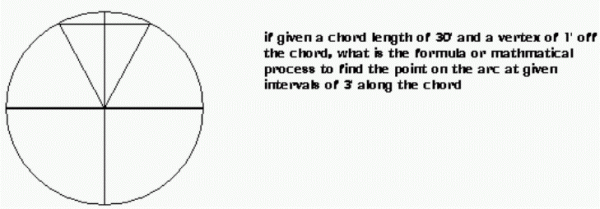 |
Hi Angela.
This is the kind of question we get from time to time from people in construction trades or even doing home carpentry, so I'll try to solve it in a general way before applying that to the figures in your question. Let's call the length of the chord C and the distance from the chord to the peak of the arc S. These are our knowns.
The reasons for this are due to the terminology of the circle:
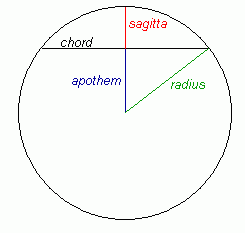
So in your case, the sagitta is 1 foot and the chord length is 30 feet.
Deriving the General Solution:
I have placed the circle on a normal cartesian graph. One end of the chord is at location (0,0) and the other end is at location (C,0). The top of the circle is at location (C/2,S).
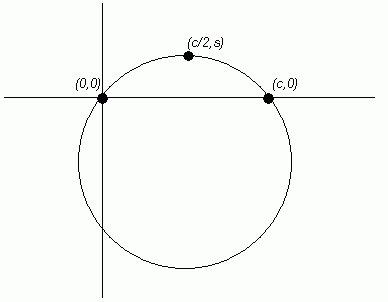
Any three points on a circle define the circle. We can write the equation of any circle in the general form:
(x - x0 )2 + (y - y0 )2 = r2
where (x0 , y0 ) is the center of the circle and r is the radius.
We don't know any of these values, but we're going to find them all with algebra.
We have three points known on the circle, so we can substitute for (x, y) for each of these points:
| (A) : (0, 0) | (B): (C, 0) | (C): (C/2, S) |
(x - x0 )2 + (y - y0 )2 = r2 (0 - x0 )2 + (0 - y0 )2 = r2 x02 + y02 = r2 |
(x - x0 )2 + (y - y0 )2 = r2 (C - x0 )2 + (0 - y0 )2 = r2 C2 - 2Cx0 + x0 2 + y0 2 = r2 |
(x - x0 )2 + (y - y0 )2 = r2 (C/2 - x0 )2 + (S - y0 )2 = r2 C2 /4 - Cx0 +x0 2 + S2 - 2Sy0 + y0 2 = r2 |
Examine equations (A) and (B): they both equal r2 , so they equal each other:
x02 + y02 = C2 - 2Cx0 + x0 2 + y0 2
0 = C2 - 2Cx0
0 = C - 2x0
x0 = C/2
Now x0 is known.
Perhaps that was obvious to you already, since of course the center of the circle must be directly below the apex of the circle. Let's continue by trying to find y0 with known values.
Equation (A) and (C) both have expressions for r2 as well, so they equal each other:
x02 + y02 = (C/2 - x0 )2 + (S - y0 )2
(C/2)2 + y02 = (C/2 - C/2 )2 + (S - y0 )2
(C/2)2 + y02 = S2 - 2Sy0 + y0 2
y0 = ( S - x02/S ) / 2
and now y0 is also known.
This means we know the center of the circle:
(x0 , y0 ) = ( C/2, (S - x0 2/S) / 2 )
Now recall that we can solve for r2 by flipping over equation (A):
r2 = x02 + y02
And when we solve the general equation of a circle for y, we get this:
(x - x0 )2 + (y - y0 )2 = r2
y2 - 2y0 y + y0 2 + (x - x0 )2 - r2 = 0
which is a quadratic equation we can solve using the quadratic formula:
ay2 + by + c = 0
y = (-b ![]() sqrt(b2 - 4ac) ] / (2a)
sqrt(b2 - 4ac) ] / (2a)
for us,
[1]y2 + [- 2y0] y + [ y0 2 + (x - x0 )2 - r2 ] = 0
a = 1
b = -2y0
c = y0 2 + (x - x0 )2 - r2
Because of the ![]() in the quadratic formula, we know we'll get two answers: one is in the top half and one is in the bottom half of the circle, but since we are interested in how high the arc is above the line, we only care about the top half. Examining the quadratic formula, you can see that we should ignore the minus and use the plus result from the
in the quadratic formula, we know we'll get two answers: one is in the top half and one is in the bottom half of the circle, but since we are interested in how high the arc is above the line, we only care about the top half. Examining the quadratic formula, you can see that we should ignore the minus and use the plus result from the ![]() in there. Since a is 1 and b = -2y0, we can simplify it:
in there. Since a is 1 and b = -2y0, we can simplify it:
y = [ 2y0 + sqrt((2y0)2 - 4c) ] / 2
y = y0 + sqrt(y02 - c)
so
y = y0 + sqrt(y02 - [y0 2 + (x - x0 )2 - r2])
y = y0 + sqrt(r2 - (x - x0 )2 )
and this produces our answer!
General Solution:
Now we have all the pieces we need to construct the general equations given any chord length (C) and sagitta (S), like in your question:
1. Find the value of x0 using x0 = C/2.
2. Find the value of y0 using y0 = (S - x0 2/S) / 2.
3. Find the value of r2 using r2 = x02 + y02.
At this point we choose where on the chord we want to know the height. This means we choose an x (such as 3 feet from the left end, or 6 inches from the right, or whatever we want) and we try to find the corresponding y, which is the height of the arc above that point on the chord. So basically, you would do the next step for EACH x you are interested in:
4. Find the value of y using y = y0 + sqrt(r2 - (x - x0 )2 ).
Angela's Question:
Now let's solve it for your question. C = 30 and S = 1 (we'll do it all in feet):
1. x0 = C/2 = 30/2 = 15
2. y0 = (S - x0 2/S) / 2 = (1 - 152 /1) /2 = -112
3. r2 = x02 + y02 = 152 + 1122 = 12769
Now let's calculate every three feet from 0 to 30 feet for x:
| x | y = y0 + sqrt(r2 - (x - x0 )2 ) |
| 0 | 0.000 |
| 3 | 0.361 |
| 6 | 0.641 |
| 9 | 0.841 |
| 12 | 0.960 |
| 15 | 1.000 |
| 18 | 0.960 |
| 21 | 0.841 |
| 24 | 0.641 |
| 27 | 0.361 |
| 30 | 0.000 |
And this solves your question.
Stephen La Rocque. >
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.