 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Anne, a parent: Assuming both sides of a coin are identical, and a line tangent to the inner circle is 23 mm from edge to edge of the coin, and excluding the edge of the coin in the calculation, what is the surface area of the coin, in square millimetres? |
Hello Anne.
When you say "inner circle", I guess you are referring to a ridge around the outside, right?
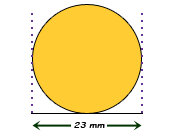Well, you know the area of a circle is calculated as A = π r2, where r is the radius of the circle and π is about 3.1416. To get the radius, you just divide the diameter in two, because the diameter is all the way across the coin and the radius is the distance from the center of the coin to the outside. So the radius is 11.5 mm.
Since you are excluding the edge (and we don't know the thickness anyway), the surface area of the coin is just this area A multiplied by 2 (front and back of the coin).
Hope this helps,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.