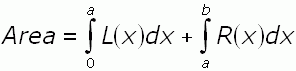Hello Apratim.

Let us consider any arbitrary triangle. Choose its longest side, call that length b and place that edge along the x-axis of a Cartesian graph, with one vertex on the origin and the other at (b, 0). Because this is the longest side, the other vertex must lie between 0 and b horizontally. If we place it above the x-axis, then we can draw this diagram:

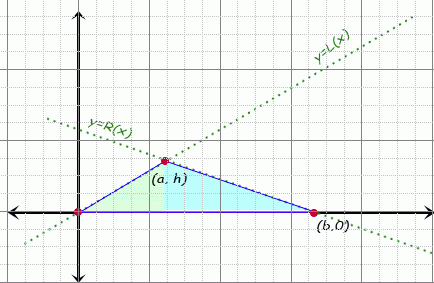
The area enclosed by the triangle is composed of two pieces:

(1) The area between the "curve" of the function from x = 0 → a and the x-axis, and

(2) The area between the "curve" of the function from x = a → b and the x-axis.

The equations of these two "curves" are linear of course.

So compute the equation of the left line, call it  L(x) and the equation of the right line, call it R(x).

Thus the area of the triangle is the sum of the definite integrals of these functions:

The right side takes a couple of steps to simplify, but it is just simple algebra and you get the correct answer (the variable a disappears and you are left with Area = ½ bh).

Hope this helps,
Stephen La Rocque.