Hi Ashley.

I've drawn what you describe and I've also drawn a few extra lines and labelled some points:

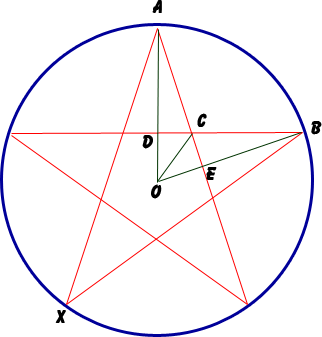I hope you can convince yourself that the area of the star in total is ten times the area of triangle CAO.

This means that COA is one-tenth of the way around the circle, so it is 36°. That means that EOD is 72°.

A property of circle geometry tells us that when you have two points (like A and B) on the circumference of a circle, the angle from the center (O) is twice the angle from a point on the circumference (X). So EOD = 2BXA.
This tells us that BXA is 72°/2 = 36°.

By symmetry, CAO is therefore 18°.

Since we know two angles of triangle CAO, we know the third: OCA = 180°-36°-18° = 126°.

And you are given that length AO is 10 cm.

Now with this information, we can find the area of the triangle:

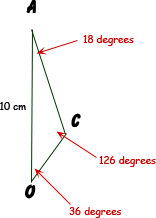At this point, you can use the Law of Sines to find the lengths of the other two sides AC and CO.

Then, with three lengths, you can use Heron's formula to find the area of the triangle CAO.

Hope this helps,
Stephen La Rocque.

PS: If you don't know these formulas, you can find more about them by using the search form for Quandaries and Queries. We've written quite a bit about both.