Hi Avaline.

Let's examine a diagram first:

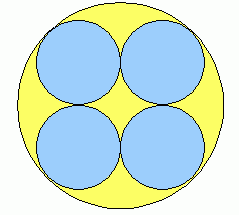
Now let's add a few dimensional lines to help analyze this figure:

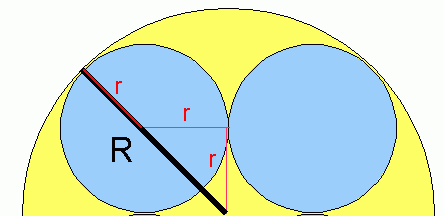
As you can see, the radius of the large circle is R and the radius of one shaded (blue) circle is r.

So the ratio of the blue-to-yellow (shaded-to-unshaded) areas is:

4πr² : (πR² - 4πr²)

This doesn't finish the problem, because we have two variables in there. Can you examine the lines I drew and come up with a relationship between r and R? Then you can substitute this in and the last variable will cancel out leaving you with a simple ratio.

Hope this helps,
Stephen La Rocque.