Benneth, we have two responses for you.

Hi Benneth.

I've drawn an arbitrary rectangle inscribed in a circle whose radius is R below:

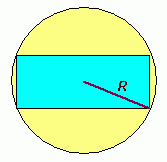
As you can see, the radius of the circle is equal to the length of the hypotenuse of a right triangle which is duplicated 8 times in the rectangle:

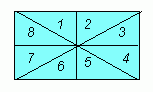
This means that the area of the rectangle is 8 times the area of one of the right triangles. And of course, each right triangle's area is simply ½bh where these variables are the base and height.

The proportionals of the triangle depend on the shape of the rectangle, of course, with the limiting sizes being an infinitely short one up to an infiinitely thin one, with the middle of the range being the square. Here's a sketch of several of them superimposed on the circle:

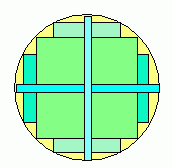
Now, the smallest area of rectangle is clearly the infinitely thin or short one, since its other dimension is basically R. This means the lowest possible area is 8(½)(0)(R) which is zero. The real question is what is the largest possible area.

Intuition should tell you that the square is the largest area and your intuition would be right, but that's not a satisfactory answer to a mathematics question. Let's look again at those triangles:

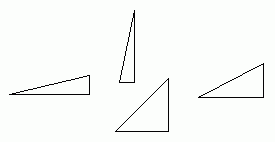
Here are several possible shapes. The hypotenuse is always R units long of course, so that means that we can use trigonometry to find the area of the triangle. Let's call the angle at the triangle's corner that is located at the center of the circle A. That's the bottom left corner in these sample triangles.

This means that the base is RcosA units long and the height is RsinA units long. That makes the area of the triangle ½R² cosA sinA. So the area of the whole rectangle is eight times this: 4R² cosA sinA. What value of A gives us the largest overall area?

For this, we can use a number of techniques, but the easiest is calculus. The critical points of this function can tell us what angle A needs to be for a maximum.

The derivative of 4R² cosA sinA is 4R² (cos²A - sin²A); I used the product rule to get this. When this is zero, we have a critical point which is the value of A for which we get maximum area.

Thus, cos²A = sin²A and therefore cosA = sinA. Since cosine is the base over the hypotenuse R and sine is the height over the hypotenuse R, this means base = height. And that means an isoceles right triangle, so the rectangle is the square. We've proven what our intuition told us long ago.

Thus, the rectangle's area is constrained between 0 and that of the square whose diagonal length is 2R.

Hope this helps,
Stephen La Rocque.

Benneth,

Actually - every rectangle can be inscribed in a (unique circle) so the key point is that the radius of the circle is R (I think).

One of the properties of a rectangle is that the diagonals bisect in the 'center' of the rectangle, which will also be the center of the circumscribing circle. Now the 'maximum' and 'minimum' are best imagined (and imaged) with a program like Geometer's Sketchpad where you can play with the options.

Rather than state an answer, let me past in a couple of samples from the program to stimulate your imagination:

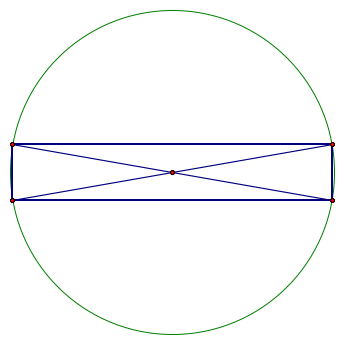
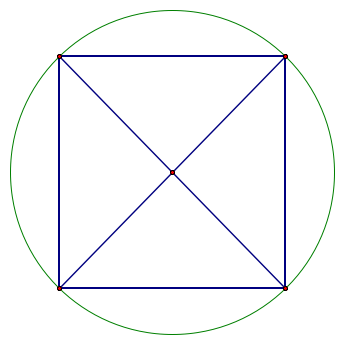
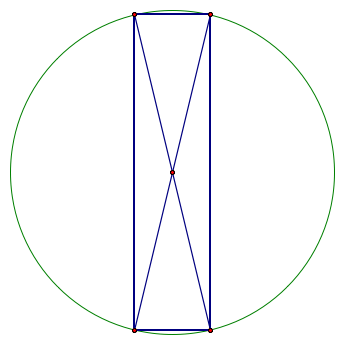
You can see that the area is getting bigger, then smaller as the corner moves around a quarter of the circle.
I think, from this, you can figure out the smallest area. The largest area is a big trickier, but again, I think you can 'see' it. If you are unsure, you can think about the maximum area for the triangle ABC (all diagonals have the same length - 2R).

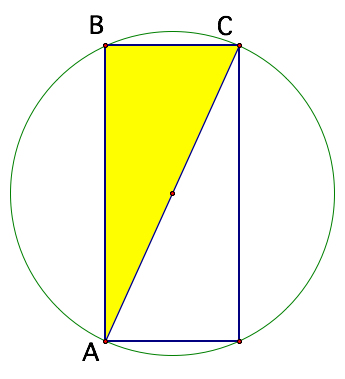
The whole rectangle is just two of these triangles. Again, if you are not quite sure, it is visually a bit more easily if you 'tilt your head' and make the diagonal AC horizontal, and think about making the 'height' of the triangle as big as possible, over this base!

Walter