Hi Bree.

I am not completely sure what you mean by "diameter": do you mean the distance between parallel sides (I've drawn that in blue in my diagram) or the distance between opposite corners (drawn in green)?

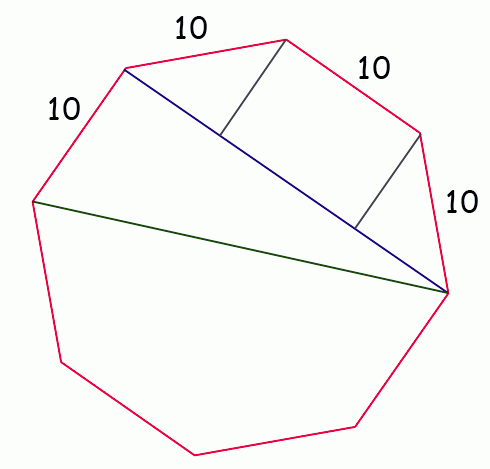
Either way, the easiest to solve is for the blue line and once you have that, you can use Pythagoras' Theorem to solve for the green line if you need it.

Notice first that the blue line is made up of three lengths: one is the same as the length of a side (10) and the other two are (by symmetry) equal to each other. These smaller pieces are in fact the legs of a right triangle. Also, I am sure you will agree that symmetry, the acute angles of the small triangle must be equal (so it is a right triangle, but also an isosceles triangle). And in an isoceles triangle, the sides opposite equal angles have equal lengths. That means instead of writing x² + y² = 10² according to Pythagoras, we can simply write x² + x² = 10². That means x = 10/.

And since 2x + 10 is the length of the blue line...you can finish this.

And since the red and green lines make a right triangle and you know the lengths of the two legs...

Hope this helps,
Stephen La Rocque.

PS: I've assumed you mean a regular octagon, of course. That is one where the angles are all equal and the sides are all equal.