Bridget, we have two responses for you:

Bridget,

it is often worth your while to look into our database (use the Quick Search) for some of your questions.  There's a comment on a more general problem than yours

mathcentral.uregina.ca/QQ/database/QQ.09.06/tania1.html

Penny

Hi Bridgit.

After looking at Penny's reply to Tania (see the link above), I thought of another way of visualizing the same problem.

Let's consider an m by n grid of squares.

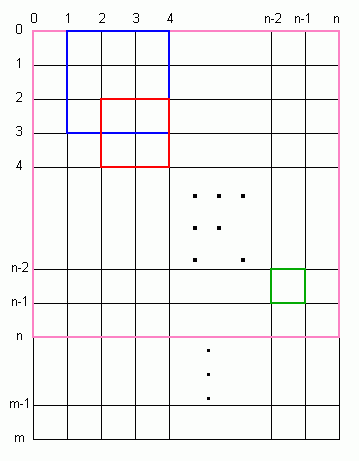
Now to find the number of squares, we do what Penny said: start counting squares of size 1, then count squares of size 2, and so on until we get up to the smaller of m or n.

Let's say that we call the shorter side n from now on in our discussion.

You can see from the diagram on the left that I've coloured just a few of the many squares that are present here. Clearly, the largest square is n by n units, but there may be several of this large size if m > n.

So to go about this systematically, we first recognize that a square has four sides, so by choosing two vertical lines spaced x units apart and two horizontal lines spaced x units apart, we identify a single square.

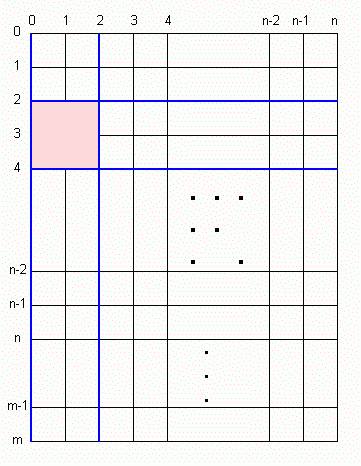
For example, if we choose vertical lines 0 and 2, then x is 2. We then choose, say, horizontal lines 2 and 4. This identifies a particular square:

So the size of the square (x) ranges from 1 to n.

That means the left line ranges from 0 to n-x.

And the top line ranges from 0 to m-x.

(The right line and the bottom line are determined by the choice of the size, the left line and the top line.)

So let's look at this in more detail:

• x = 1:
  • Left line: (n+1) - 1 = n possible choices.
  • Top line: (m+1) - 1 = m possible choices.
  • Total number of size 1 squares: nm.
• x = 2:
  • Left line: (n+1) - 2 = n - 1 possible choices.
  • Top line: (m+1) - 2 = m - 1 possible choices.
  • Total number of size 2 squares: (n - 1) (m - 1).
• x = 3:
  • Left line: (n+1) - 3 = n - 2 possible choices.
  • Top line: (m+1) - 3 = m - 2 possible choices.
  • Total number of size 3 squares: (n - 2) 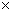(m - 2).
• and so on, until finally x = n:
  • Left line: (n+1) - n = 1 possible choice.
  • Top line: (m+1) - n = m - n + 1 possible choices.
  • Total number of size n squares: (m - n + 1).

So the total number of squares is the sum of all this:

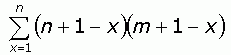
If we multiply this out, we get:

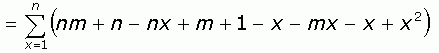
And then let's group the terms and break the summation into three parts:

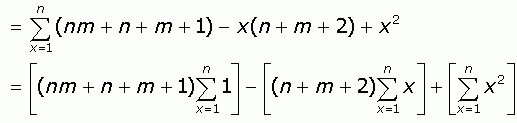
The rest is easy. You probably know already these three standard sums:

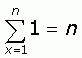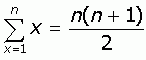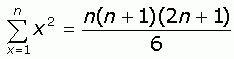So you can substitute these in.

For your particular question Bridget, n = m = 4, so we have

( (4)(4) + 4 + 4 + 1)(4) - (4 + 4 + 2) (4) (4 + 1) / 2 + (4)(4 + 1)(2(4) + 1) / 6

100 - 100 + 30 = 30 squares.

Something very curious happened here! The first two of the three parts cancelled each other out! This always works when n = m, an assumption we didn't make in our general solution, but since you started with a 4 by 4 square, it makes sense that the answer for an n by n square is just

In other words, the total of all the squares in a square is the sum of all the squares !

LOL,
Stephen La Rocque.